Trong lớp học có một số ghế dài. Nếu xếp mỗi ghế bốn học sinh thì có bảy học sinh không có chỗ. Nếu xếp mỗi ghế năm học sinh thì còn thừa một ghế. Hỏi lớp có bao nhiêu ghế và bao nhiêu học sinh?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 2 2021
Đặt số ghế là x; số học sinh là y ta có hệ phương trình
\(\hept{\begin{cases}4x=y-6\\\frac{y}{5}=x-1\end{cases}}\)
Bạn tự giải nốt hệ nhé
CM
28 tháng 8 2018
Gọi số ghế trong phòng học là x (ghế), số học sinh của lớp là y (học sinh). Điều kiện x, y ∈N*
Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ, ta có phương trình: 3x + 6 = y
Nếu xếp mỗi ghế 4 học sinh thì thừa một ghế, ta có phương trình: (x – 1)4=y
Ta có hệ phương trình:
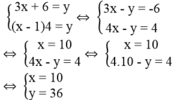
Giá trị của x và y thỏa điều kiện bài toán.
Vậy trong phòng học có 10 ghế và 36 học sinh.
AH
Akai Haruma
Giáo viên
8 tháng 1 2022
Lời giải:
Giả sử trong phòng học có $a$ học sinh.
Theo bài ra, nếu xếp mỗi bộ bàn ghế 3 hs thì số bộ bàn ghế là:
$\frac{a-4}{3}$ (bộ)
Nếu xếp mỗi bộ bàn ghế 4 học sinh thì số bộ bàn ghế là:
$\frac{a-2}{4}$ (bộ)
Số bộ bàn ghế không đổi nên: $\frac{a-4}{3}=\frac{a-2}{4}$
$\Rightarrow a=10$ (hs)
Số bộ bàn ghế là: $\frac{a-2}{4}=\frac{10-2}{4}=2$ (bộ)
31 tháng 3 2020
gọi số học sinh là x(hs;x∈N*)
số ghế dài là y(ghế;y∈N*)
vì khi xếp mỗi ghế 3 học sinh thì 6 học sinh không có ghế ngồi
nên ta có phương trình x -3y = 6(1)
vì xếp mỗi ghế 4 học sinh thì thừa 1 ghế
ta có pt x = 4(y-1)
<=> x - 4y = -4(2)
từ (1)(2)ta có hpt
x-3y=6 và x-4y = -4 <=> x =36 ; y=10(tm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
29 tháng 7 2023
4 học sinh trên 1 bộ hơn 6 học sinh trên 1 bộ là:
6 - 4 = 2 (học sinh)
Tất cả số bộ bàn ghế mỗi bộ xếp 6 học sinh nhiều hơn tất cả các bộ bàn ghế mỗi bộ xếp 4 học sinh là:
4 x 2 + 6 x 2 = 20 (học sinh)
Số bộ bàn ghế là: 20 : 2 = 10 (bộ)
Số học sinh là: (10 + 2) x 4 = 48 (học sinh)
Đáp số: 10 bộ bàn ghế
48 học sinh
Thử lại ta có xếp mỗi bộ bàn ghế 4 học sinh thì cần:
48 : 4 = 12 (bộ)
So với thực tế thì thiếu 12 - 10 = 2 (bộ) ok
Xếp mỗi bộ bàn ghế mỗi bộ 6 học sinh thì cần:
48 : 6 = 8 (bộ)
So với thực tế thì thừa 10 - 8 = 2 (bộ) ok
vậy kết quả là đúng
Gọi số ghế và số học sinh của lớp lần lượt là \(x,y\left(x,y\inℕ^∗\right)\)
Nếu xếp mỗi ghế 4 học sinh thì 7 học sinh không có chổ, vì vậy ta có phương trình \(4x+7=y\)\(\Leftrightarrow y-4x=7\)(1)
Nếu xếp mỗi ghế 5 học sinh thì còn thừa 1 ghế, nên ta có phương trình \(\frac{y}{5}+1=x\Leftrightarrow y+5=5x\Leftrightarrow5x-y=5\)(2)
Từ (1) và (2) ta có hệ phương trình \(\hept{\begin{cases}y-4x=7\\5x-y=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x+7\\5x-\left(4x+7\right)=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x+7\\x=12\left(nhận\right)\end{cases}}\Leftrightarrow\hept{\begin{cases}y=55\left(nhận\right)\\x=12\end{cases}}\)
Vậy lớp có 12 ghế và 55 học sinh.