Cho hình chóp S ABCD . có đáy ABCD là hình bình hành tâm O. Gọi M.N.P lần lượt là trung điểm AD,BC và SB a, tìm giao điểm Q của SA và (MNP) b, chứng minh SD//(MNP) và (SMC)//(ANP) c, gọi H=BD ∩ AN, K=BD ∩ MC, i= PK ∩ SH. tính tỉ số SΔSLK/SΔSLP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong mp (ABCD), nối NP kéo dài cắt AD tại G
Trong mp (SAD), nối MG cắt SD tại Q
\(\Rightarrow Q=SD\cap\left(MNP\right)\)
b.
Trong mp (ABCD), gọi E là giao điểm NP và AC
Trong mp (SAC), nối ME cắt SO tại F
\(\Rightarrow F=SO\cap\left(MNP\right)\)

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)
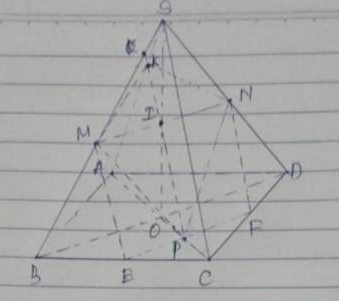


a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)
Gọi Q là trung điểm SA
\(\Rightarrow PQ\) là đường trung bình tam giác SAB
\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SA\cap\left(MNP\right)\)
b. Do Q là trung điểm SA, M là trung điểm AD
\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)
Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)
Tương tự ta có \(NP||SC\) (đường trung bình) (1)
\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)
(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)
c. Đề bài không tồn tại điểm L