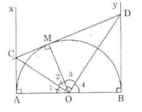
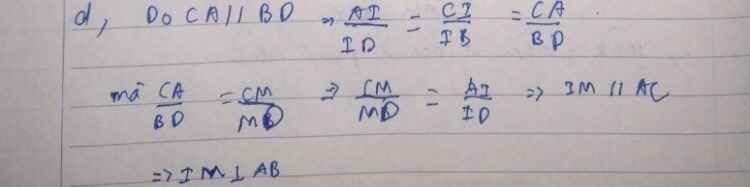Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F
a) chứng minh BDCF là tứ giác nội tiếp đường tròn
b) chứng minh CD2 =CE.CF
c) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB
d) Khi EF là tiếp tuyến của nửa đường tròn đường kính AB thì D nằm ở vị trí nào trên AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB

Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).

TK:
a.
xét tứ giác BDMI ta có : IMD = 90 (CD ⊥ MI)
IBD = 90 (BD là tiếp tuyến)
mà 2 góc này ở vị trí đối nhau ⇒tứ giác BDMI là tứ giác nội tiếp
⇒ DMB = DIB (2 góc nội tiếp cùng chắng cung DB của tứ giác BDMI) (1)
xét tứ giác ACMI ta có : IAC = 90 (AC là tiếp tuyến)
IMC = 90 (CD ⊥ MI)
mà 2 góc này ở vị trí đối nhau ⇒⇒ tứ giác ACMI là tứ giác nội tiếp
⇒ CMA = CIA (2 góc nội tiếp cung chắng cung AC của tứ giác ACMI) (2)
mà CMA + DMB = 90 (góc AMB là góc nội tiếp chắng nửa (o)) (3)
tứ (1) ; (2) và (3) ta có : CIA + DIB = 90
⇒ CID = 180 - 90 = 90
xét tứ giác MIEF ta có : AMB = 90 (góc nội tiếp chắng nửa (o))
CID = 90 (chứng minh trên)
mà 2 góc này ở vị trí đối nhau ⇒ tứ giác MIEF là tứ giác nội tiếp (đpcm)

a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc AOM
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc BOM
=>\(\widehat{BOM}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>OC\(\perp\)OD
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
\(\dfrac{AC^2+BD^2}{CD^2}\)
\(=\dfrac{AC^2+\left(3AC\right)^2}{\left(CM+MD\right)^2}\)
\(=\dfrac{10AC^2}{\left(CA+BD\right)^2}\)
\(=\dfrac{10AC^2}{\left(AC+3AC\right)^2}=\dfrac{10}{4^2}=\dfrac{10}{16}=\dfrac{5}{8}\)