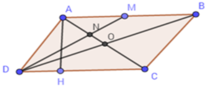
Cho hình bình hành ABCD và điểm M là trung điểm của AB. Hai đoạn thẳng AC và DM cắt nhau tại E.
a) Tính diện tích hình tam giác MEC biết diện tích hình tam giác MBC bằng 15 cm2.
b) Gọi điểm N là trung điểm của cạnh CD, nối BN cắt AC tại G. Chứng tỏ rằng AE = EG = GC

Giải thích các bước giải:
a) Xét tam giác ABC và AMC có chung chiều cao hạ từ đỉnh C mà M là trung điểm AB nên AB = 2 x AM => S_ABC = 2 x S_AMC
Xét tam giác AMC với AMD có chung đáy AM, chiều cao hạ từ đỉnh D đáy AM = chiều cao từ đỉnh C đáy AM => S_AMC = S_AMD.
b) Nối AN và EN
Xét các tam giác AMC và ANC đều = 1/4 diện tích hình bình hành = 15 cm2. Mặt khác 2 tam giác này có chung đáy AC => chiều cao hạ từ đỉnh M xuống đáy AC = chiều cao từ đỉnh N đáy AC.
Xét tam giác ENC và EMC chung đáy EC, chiều cao bằng nhau => S_ENC = S_EMC. (1)
Xét tam giác EDN và ENC chung đỉnh E, đáy DN = NC => S_EDN = S_ENC (2)
Xét S tam giác AMD = S_AMC (phần a đã chứng minh) có chung AME => S_AED = S_EMC (3)
Từ (1) ; (2) và (3) => S_EMC = S_ENC = S_EDN = S_AED.
Ta có S_MBC = 15 cm2 => S_ACD = 15 x 2 = 3 (cm2)
Mà S_ACD = S_ENC + S_EDN + S_AED và 3 tam giác này bằng nhau nên :
S_ENC = 30 : 3 = 10 (cm2) mà S_ENC = S_MEC.
Vậy diện tích MEC = 10 cm2.
c) Từ S_MEC = 10 cm2 => S_MEA = 15 - 10 = 5 (cm2)
Xét có chung chiều cao đỉnh M mà S_MEA/S_MCA = 5/15 = 1/3 =>đáy AE = 1/3 AC
(với cách chứng minh tương tự ta có S_NGC = 5 cm2 và GC = 1/3 AC)
Vậy EG = AC - 1/3 AC - 1/3 AC = 1/3AC
Vậy AE = EG = GC