Giải giúp em bài 3 này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)



\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)



\(\left|x+\dfrac{1}{7}\right|-\dfrac{2}{3}=0\)
\(\Rightarrow\left|x+\dfrac{1}{7}\right|=0+\dfrac{2}{3}\\ \Rightarrow\left|x+\dfrac{1}{7}\right|=\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{7}=\dfrac{2}{3}\\x+\dfrac{1}{7}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-\dfrac{1}{7}\\x=-\dfrac{2}{3}-\dfrac{1}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{21}\\x=-\dfrac{17}{21}\end{matrix}\right.\)

Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)


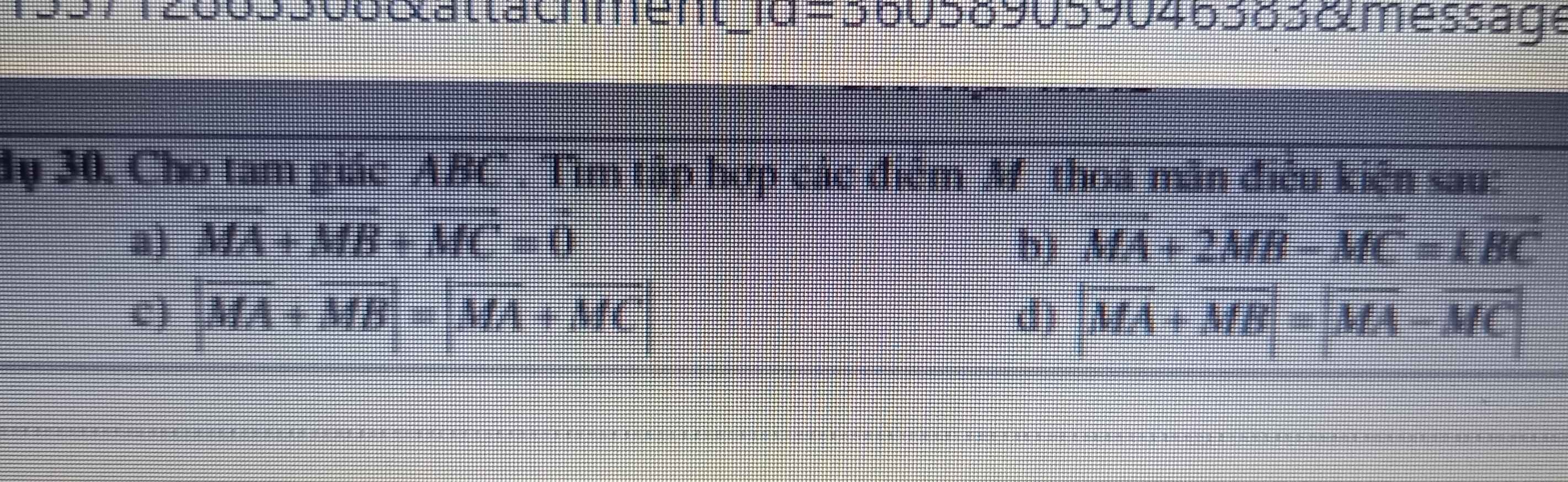
 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ


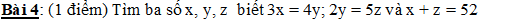
Đáp án C
Hi, mình bày bạn cách bấm máy tính nhé.
- Trước tiên bạn xác định đề bài, điều kiện x nằm ở đâu. Bạn chọn 1 số bất kì trong khoảng x thuộc. (Ở đây mình chọn x=3)
- Tiếp theo bạn phải hiểu được f(x) là đạo hàm của 1 trong 4 đáp án. Nghĩa là, khi bạn đạo hàm 1 trong 4 đáp án bạn sẽ nhận được f(x)
- Tiếp theo bạn nhập hàm f(x) vào máy tính, bấm CALC, gán cho x=3, bạn sẽ nhận được f(3)=6
- Tiếp tục, bạn nhập lần lượt đạo hàm của các đáp án A,B,C,D vào và cho x=3. Bạn dò xem 1 trong 4 đáp án đó, cái nào thỏa được bằng 6 thì đó là nguyên hàm của f(x). (Ở đây mình nhận được đáp án C có giá trị bằng 6 khi x=3)
Mình cảm ơn cái này thầy mình chưa có dậy qua ý nên kbt làm như thế nào huhu cảm ơn cậu nhiều ạ