Cho đường tròn tâm O bán kính R và đường thẳng (d) không qua O, cắt đường tròn (O) tại 2 điểm A, B. Lấy điểm M bất kì trên tia đối của tia BA, qua M kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là tiếp điểm)
1. Chứng minh tứ giác MCOD nội tiếp trong một đường tròn.
2. Gọi H là trung điểm của AB. Chứng minh HM là phân giác của góc CHD

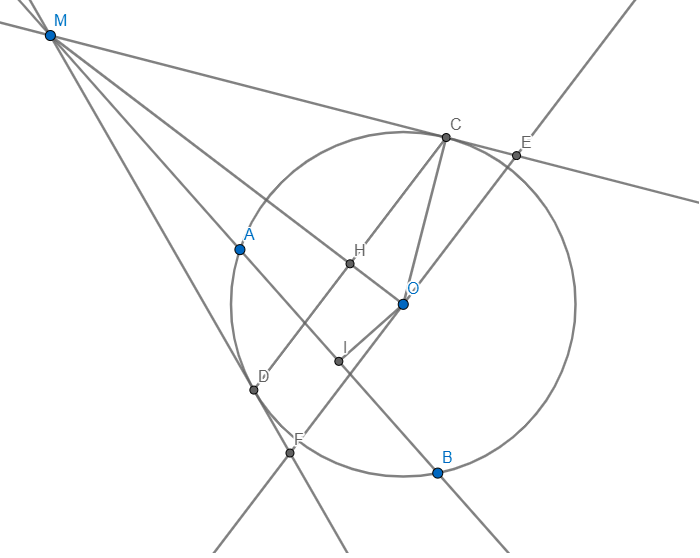

Giải ntn ạ