giúp mình bài 5 vs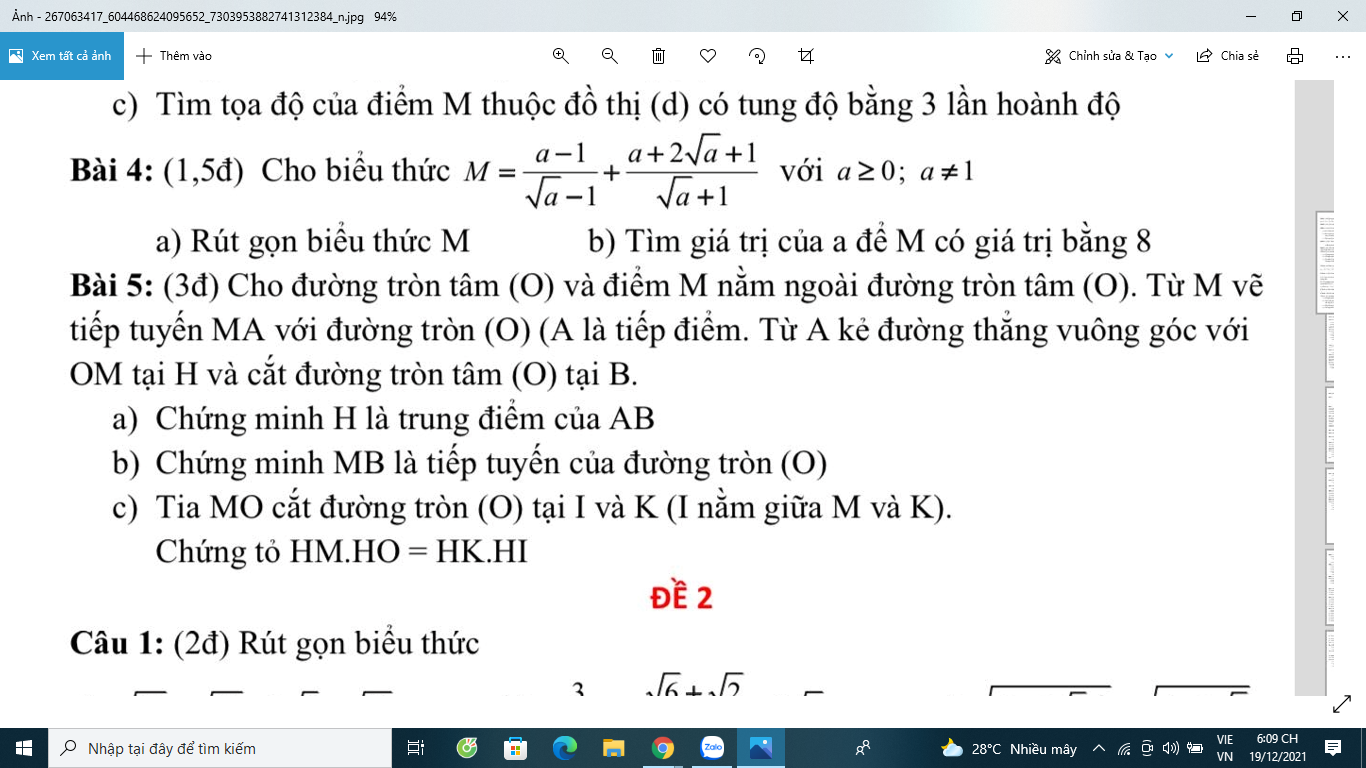
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,A=x^2-6x-2=\left(x-3\right)^2-11\ge-11\)
Dấu \("="\Leftrightarrow x=3\)
\(b,B=6x-9x^2+2=-\left(3x-1\right)^2+3\le3\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{3}\)

Áp dụng BĐT Bunhiacopxki cho 2 bộ số (\(\sqrt{a+b}\),\(\sqrt{b+c}\),\(\sqrt{a+c}\)) và (1,1,1) có: (1.\(\sqrt{a+b}\)+1.\(\sqrt{b+c}\)+1.\(\sqrt{a+c}\))2 ≤ (a + b + b + c + c + a)(12 + 12 + 12)
=> S2 ≤ 2.3 = 6 ⇔ S ≤ \(\sqrt{6}\)
Dấu "=" xảy ra ⇔ \(\sqrt{a+b}\) = \(\sqrt{b+c}\) = \(\sqrt{a+c}\) ⇔ a +b = b + c = c + a
⇔ 1 - c = 1 - a = 1 - b
⇔ a = b = c = \(\dfrac{1}{3}\)
Vậy maxS = \(\sqrt{6}\) ⇔ a = b = c = \(\dfrac{1}{3}\)

5:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
b: \(MA=\sqrt{OM^2-OA^2}=R\sqrt{3}\)
=>\(AH=\dfrac{R\cdot R\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
=>\(AB=R\sqrt{3}\)

(x+5)(x+2) -3(4x-3)=(5-x)^2
(=) x^2+2x+5x+10-12x+9=5^2-2*5x+x^2
(=) x^2+2x+5x-12x+25x-x^2+10x=-10-9+25
(=) 30x=6
(=) x= 1/5=0,2

Số các số hạng của dãy số trên là:
81:(1+3+5)=9 số hạng
=> ta có dãy số như sau:
1+3+5+7+9+11+13+15+17
Vậy X là số hạng cuối cùng nên X=17
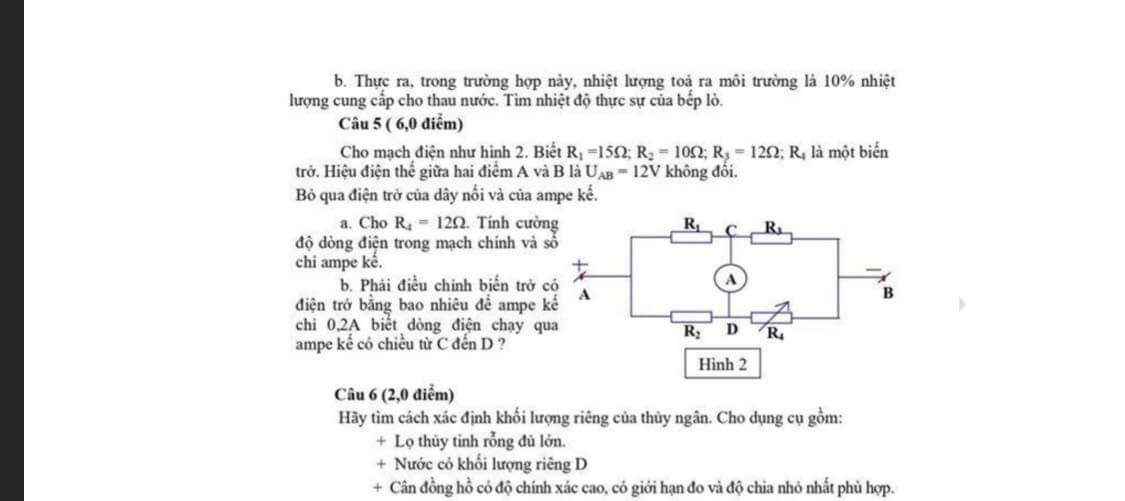




 giúp mình câu b bài 5 vs câu b bài 6 đi
giúp mình câu b bài 5 vs câu b bài 6 đi
Bài 4:
a: \(M=\sqrt{a}+1+\sqrt{a}+1=2\sqrt{a}+2\)
mình hỏi bài 5 mà bạn