*Thức hiện phép tính*
Mn ơi ,giúp em với ạ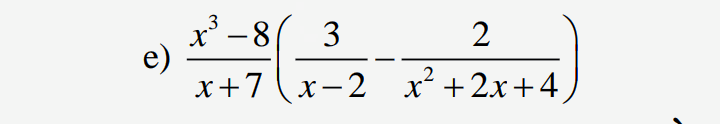 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
23 tháng 9 2021
1. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất giao hoán của phép cộng số tự nhiên?
- Lí thuyết: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
- Công thức: a + b = b + a
- VD: 2 + 3 = 3 + 2
2. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất kết hợp của phép cộng số tự nhiên?
- Lý thuyết: Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
- Công thức: (a + b) + c = a + (b + c)
- VD: (4 + 5) + 3 = 4 + (3 + 5)
3. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất cộng với số 0 của phép cộng số tự nhiên?
- Lý thuyết: Bất kì số tự nhiên nào cộng với 0 cũng bằng chính số đó
- Công thức: a + 0 = 0 + a = a
- VD: 8 + 0 = 0 + 8 = 8
Bài tập.
Vận dụng các tính chất của phép cộng thực hiện các phép tính
a) 12 + 88 + 56
= (12 + 88) + 56
= 100 + 56
= 156
b) 12 + 56 + 88
= (12 + 88) + 56
= 100 + 56
= 156
c) 204 – 204 + 2021
= (204 - 204) + 2021
= 0 + 2021
= 2021
d) 132 + 237 + 868 + 763
= (132 + 868) + (237 + 763)
= 1000 + 1000
= 2000
e) 29 + 132 + 237 + 868 + 763
= 29 + (132 + 868) + (237 + 763)
= 29 + 1000 + 1000
= 29 + 2000
= 2029
g) 652 + 327 + 148 + 15 + 73
= (652 + 148) + (327 + 73) + 15
= 800 + 400 + 15
= 1200 + 15
= 1215
LT
23 tháng 9 2021
a 156 b 156 c 2021 d 2000 e 2029 g 1215 sorry anh ko có nhiều thời gian nên chỉ viết dc kết quả thôi
VT
2
19 tháng 10 2021
\(a,=-15x^3+10x^4+20x^2\\ b,=2x^3+2x^2+4x-x^2-x-2=2x^3+x^2+3x-2\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
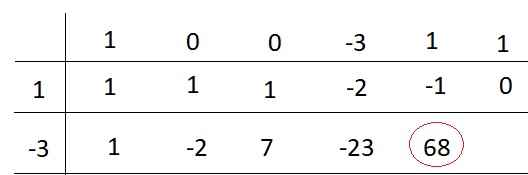
Nếu thực hiện chia theo lược đồ Hoocne thì kết quả như thế này:
\(f\left(x\right)=\left(x^2+2x-3\right)\left(x^3-2x^2+7x-23\right)+68\)
Hay \(f\left(x\right)\) chia \(x^2+2x-3\) được thương \(x^3-2x^2+7x-23\) và dư \(68\)
T
2
12 tháng 12 2021
Câu c mình làm rồi: Mn ơi, hướng dẫn em cách để giống mẫu đi ạ! - Hoc24
\(d,\dfrac{x}{x^3-27}=\dfrac{x}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x+2}{x^2-6x+9}=\dfrac{x+2}{\left(x-3\right)^2}=\dfrac{\left(x+2\right)\left(x^2+3x+9\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x-1}{x^2+3x+9}=\dfrac{\left(x-1\right)\left(x-3\right)^2}{\left(x-3\right)^2\left(x^2+3x+9\right)}\)
\(f,\dfrac{x+2}{x^2-3x+2}=\dfrac{x+2}{\left(x-1\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\\ \dfrac{x}{-2x^2+5x-3}=\dfrac{-x}{\left(2x-3\right)\left(x-1\right)}=\dfrac{-x\left(x-2\right)}{\left(2x-3\right)\left(x-1\right)\left(x-2\right)}\\ \dfrac{2x+1}{-2x^2+7x-6}=\dfrac{-\left(2x+1\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{-\left(2x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)}{\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(x+2a\right)\left(3x-2a\right)}\)
Do đó ta quy đồng:
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
20 tháng 12 2021
c: \(=\dfrac{x^3+2x+2x^2+2x+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x^2+2x+1}{x^2-x+1}\)
LT
2
Z
13 tháng 11 2021
a, 23 + ( -77 ) + ( -23 ) + 77
= [ 23 + ( -23 ) ] + [ ( -77 ) + 77 ]
= 0 + 0 = 0
b, ( -2020 ) + 2021 + 21 + ( -22 )
= ( - 2020 ) + 2021 + 21 + ( -21 ) + ( -1 )
= [ ( -2020 ) + 2021 + ( -1 ) ] + [ 21 + ( -21 ) ]
= 0 + 0 = 0
\(\dfrac{x^3-8}{x+7}\left(\dfrac{3}{x-2}-\dfrac{2}{x^2+2x+4}\right)\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\left(\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\right)\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\left(\dfrac{3x^2+6x+12}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2x-4}{\left(x-2\right)\left(x^2+2x+4\right)}\right)\)
\(=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}.\dfrac{3x^2+6x+12-2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3x^2+4x+16}{x+7}\)
\(=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x+7}\cdot\dfrac{3x^2+6x+12-2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3x^2+4x+16}{x+7}\)