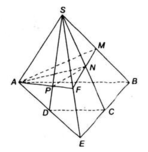
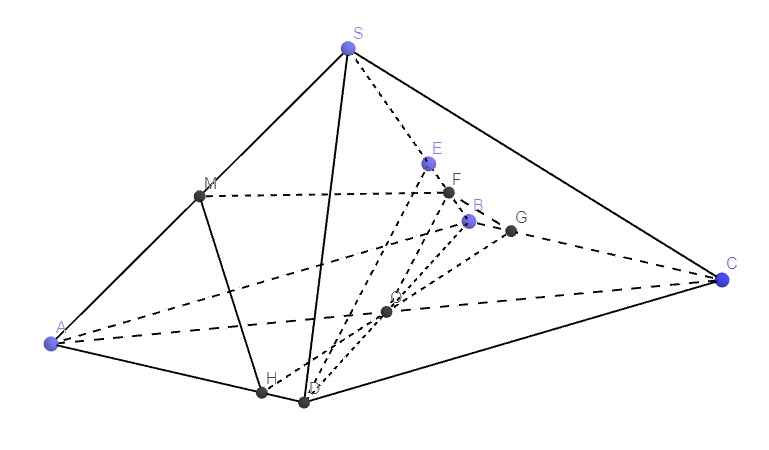
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của các đoạn SB, SC, SA.
a) Tìm giao điểm giữa PN và (BDI), với I là trung điểm của NC
b) Tìm thiết diện hình chóp cắt bởi (CMP) mai kt r chỉ mình cách làm bài này

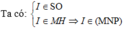

a/
Gọi O là giao của AC và BD
Trong mp (SAC) Nối PN \(\Rightarrow PN\in\left(SAC\right)\) (1)
Trong mp (BDI) Nối OI có
\(O\in AC;AC\in\left(SAC\right)\Rightarrow O\in\left(SAC\right)\)
\(I\in SC;SC\in\left(SAC\right)\Rightarrow I\in\left(SAC\right)\)
\(\Rightarrow OI\in\left(SAC\right)\)(2)
Ta có
\(O\in BD;BD\in\left(BDI\right)\Rightarrow O\in\left(BDI\right);I\in\left(BDI\right)\Rightarrow OI\in\left(BDI\right)\)
Từ (1) và (2) => PN cắt OI gọi K là giao của PN với OI
Ta có
\(K\in PN\)
\(K\in OI;OI\in\left(BDI\right)\Rightarrow K\in\left(BDI\right)\)
=> K là giao của PN với (BDI)
b/
\(PM\in\left(SAB\right);PM\in\left(CMP\right)\) => PM là giao tuyến của (SAB) với (CMP) (1)
\(CM\in\left(SBC\right);CM\in\left(CMP\right)\) => CM là giao tuyến của (SBC) với (CMP) (2)
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\) và \(O\in\left(SAC\right);O\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
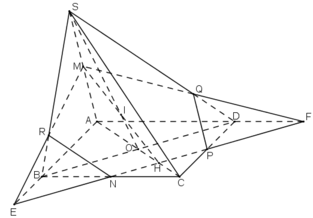
Trong mp (SAC) nối CP => CP cắt SO tại H
Ta có \(H\in SO;SO\in\left(SBD\right)\Rightarrow H\in\left(SBD\right)\)
Trong mp (SBD) nối MH cắt SD tại L
Ta có
\(MH\in\left(CMP\right);L\in MH\Rightarrow L\in\left(CMP\right)\Rightarrow PL\in\left(CMP\right);PL\in\left(SAD\right)\) => PL là giao tuyến (SAD) với (CMP) (3)
Ta có \(CL\in\left(CMP\right);CL\in\left(SCD\right)\) => CL là giao tuyến của (SCD) với (CMP) (4)
Từ (1) (2) (3) (4) => thiết diện của S.ABCD với (CMP) là tứ giác CMPL