Bài 23. Cho góc nhọn xOy. Lấy điểm A thuộc tia Ox, lấy điểm B thuộc tia Oy sao cho
OA = OB. Qua A kẻ đường thằng vuông góc với Ox cắt Oy tại M, qua B kẻ đường thẳng
vuông góc với Oy cắt Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của
MN. Chứng minh rằng:
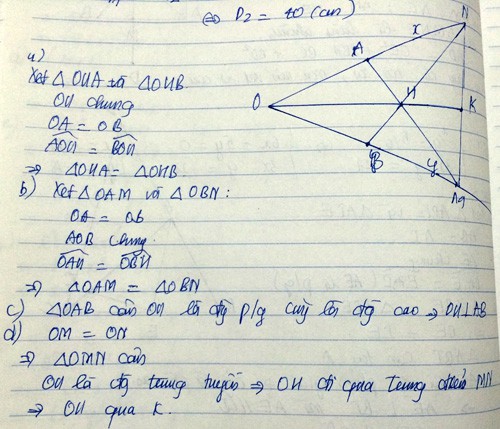
a) ON = OM và AN = BM
b) ΔANH=ΔBMH
c) Tia OH là tia phân giác của góc xOy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2021
a: Xét ΔOBN vuông tại B và ΔOAM vuông tại A có
OB=OA
\(\widehat{O}\) chung
Do đó: ΔOBN=ΔOAM
Suy ra: ON=OM
13 tháng 12 2021
a) Xét tam giác OAM và tam giác OBN có:
+ OA = OB (gt).
+ ^NOM chung.
+ ^OAM = ^OBN (= 90o).
=> Tam giác OAM = Tam giác OBN (c - g - c).
=> OM = ON (2 cạnh tương ứng).
b) Xét tam giác ANM vuông tại A và tam giác BMN vuông tại B:
+ MN chung.
+ AM = BN (Tam giác OAM = Tam giác OBN).
=> Tam giác ANM vuông tại A = Tam giác BMN vuông tại B (cạnh huyền - cạnh góc vuông).
1 tháng 4 2022
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
Suy ra OM=ON
b: Xét ΔBHM vuông tại B và ΔAHN vuông tại A có
BM=AN
\(\widehat{BHM}=\widehat{AHN}\)
Do đó: ΔBHM=ΔAHN
Suy ra: HN=HM
mà OM=ON
và IM=IN
nên O,H,I thẳng hàng