Cho tam giác ABC vuông tại A AB lớn hơn AC đường cao AH Gọi E F lần lượt là hình chiếu của H trên AB AC a. Chứng minh AE x AB = AF x AC b. Vẽ đường tròn tâm O đường kính BC Chứng minh A thuộc đường tròn tâm O c. Gọi M là trung điểm của AC tiếp tuyến của O tại A cắt tia OM tại N Chứng minh NC là tiếp tuyến của đường tròn tâm O tại C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 3 2019
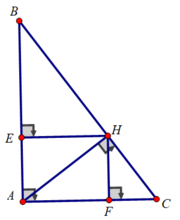
b) Xét tam giác ABH vuông tại H có HE là đường cao
⇒ AE.AB = AH2 (1)
Xét tam giác AHC vuông tại H có HF là đường cao
⇒ AF.AC = A H 2 (2)
Từ (1) và (2) ⇒ AE.AB = AF.AC
CH
5 tháng 11 2023
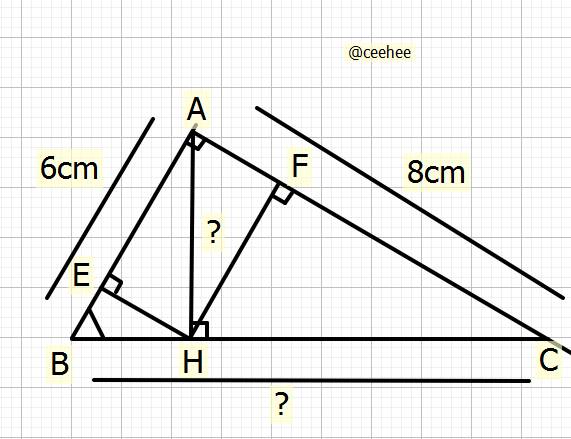
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
26 tháng 10 2023
Để chứng minh ADEF là hình chữ nhật, ta cần chứng minh các đẳng thức đường cao AH = trung tuyến AE và hình chiếu D, F của E trên AB, AC vuông góc với AB, AC.
a) Chứng minh AH = AE: Vì tam giác ABC là tam giác vuông tại A, nên đường cao AH cũng là đường cao của tam giác vuông ABC. Do đó, ta có AH = BH. Từ tam giác ABC, ta có AE là trung tuyến nên AE = EC. Vậy, AH = AE.
b) Chứng minh AD = AF: Ta có hai tam giác vuông ADE và AFE có cạnh chung AE. Vì AE là trung tuyến nên ta có DE = FE, và góc ADE = góc AFE = 90 độ (do DE và FE vuông góc với AB, AC). Do đó, ta có hai tam giác ADE và AFE đồng dạng (cạnh góc). Từ đó suy ra, AD = AF.
Vì AH = AE và AD = AF, nên tứ giác ADEF là hình chữ nhật.
c) Chứng minh BDFE là hình bình hành: Ta đã chứng minh được AD = AF, nên BD = BF (do AB < AC). Vì DE = EF (vì trung tuyến), và góc EDF = góc EBF = 90 độ (hình chiếu của E trên AB, AC vuông góc với AB, AC), nên ta có hai cạnh và một góc tương đương nhau. Do đó, tứ giác BDFE là hình bình hành.
d) Chứng minh F là trung điểm của AC: Vì AE là trung tuyến của tam giác ABC, nên F là trung điểm của AC.
Vậy, ta đã chứng minh được các yêu cầu đề bài.
16 tháng 3 2022
a, Xét tam giác HBA và tam giác ABC có
^B _ chung ; ^HBA = ^BAC = 900
Vậy tam giác HBA ~ tan giác ABC (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{24}{5}cm\)
\(\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{36}{10}=\dfrac{18}{5}cm\)
c, -bạn tự cm nhé
tam giác AEH ~ tam giác HEB (g.g)
\(\dfrac{AE}{HE}=\dfrac{HE}{BE}\Rightarrow HE^2=AE.BE\)
tam giác AFH ~ tam giác HFC (g.g)
\(\dfrac{AF}{HF}=\dfrac{FH}{FC}\Rightarrow FH^2=AF.FC\)
Cộng vế với vế ta được \(HE^2+FH^2=EF^2\)( theo định lí Pytago )
6 tháng 1 2022
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC