Giúp mình bài 3, 4 gấp. Mình sắp thi rồi. Pl/s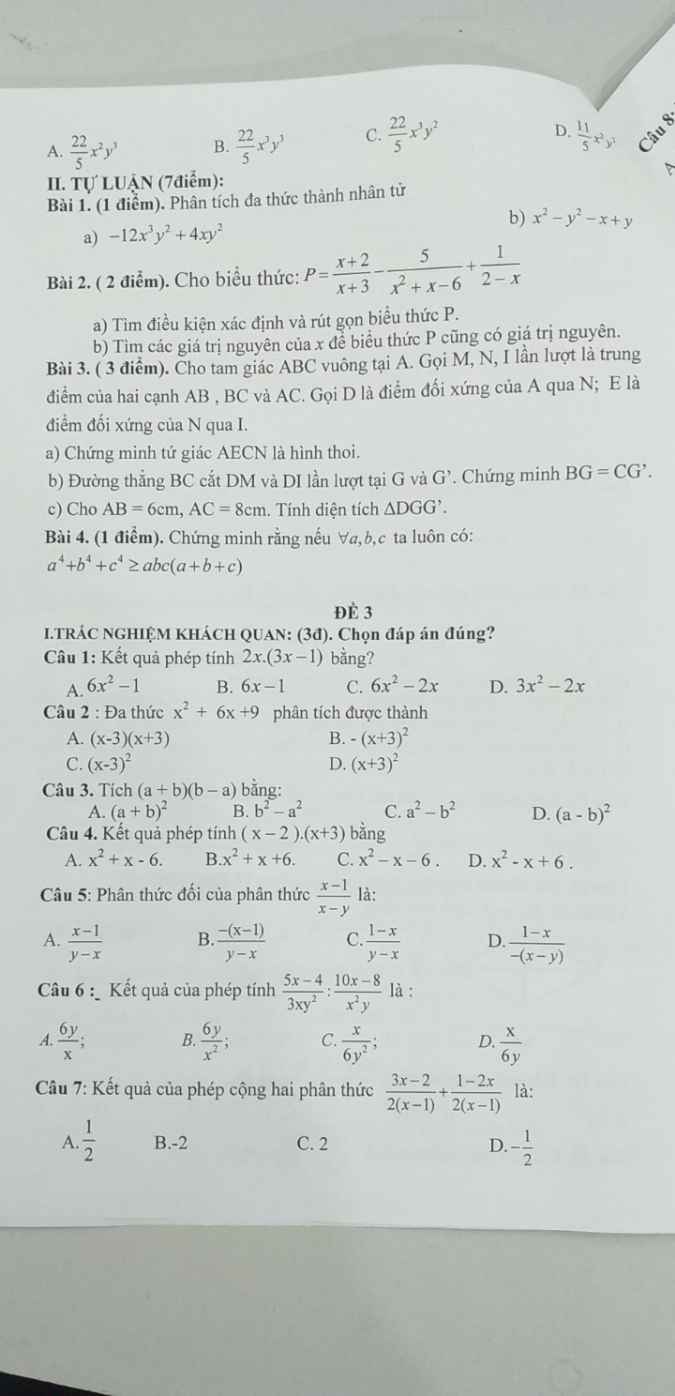
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a,trên cùng một nửa mặt phẳng bờ chứa tia Ox ta có:
góc xOy>góc xOz (80độ>30độ)
=>Oz nằm giữa hai tia Ox,Oy
b,vì Oz nằm giữa hai tia Ox,Oy
góc zOy+góc zOx=góc yOx
góc zOy+30độ=80độ
góczOy =80độ-30độ
góc zOy =50độ
c,vì góc yOt và góc xOy là góc kề bù
góc yOt + góc yOx=180độ
góc yOt+80độ=180 độ
góc yOt =180 độ -80độ
góc yOt =100độ
vì góc zOt và góc zOx là góc kề bù
góc zOt+góc zOx=180độ
góc zOt+30 độ=180độ
góc zOt =180 độ -30độ
góc zOt =150độ
a)Vì Oy, Oz nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox
Mà \(\widehat{xOz}< \widehat{xOy}\)
Do đó tia Oz nằm giữa hai tia Ox và Oy.
b)\(\widehat{zOy}=\widehat{xOy}-\widehat{xOz}=80^o-30^o=50^o.\)
c) Ot là tia đối của tia Ox nên \(\widehat{xOy}+\widehat{yOt}=180^o\)
Vậy \(\widehat{yOt}=180^o-\widehat{xOt}=180^o-80^o=100^o\)
\(\widehat{zOt}=\widehat{zOy}+\widehat{yOt}=50^o+100^o=150^o.\)

Chúc em học tốt!


Bài 4 :
\(n_{CO_2}=\dfrac{3.3}{44}=0.075\left(mol\right)\Rightarrow m_C=0.075\cdot12=0.9\left(g\right)\)
\(n_{H_2O}=\dfrac{1.8}{18}=0.1\left(mol\right)\Rightarrow n_H=0.1\cdot2=0.2\left(mol\right)\)
\(n_O=\dfrac{1.5-0.9-0.2}{16}=0.025\left(mol\right)\)
CTHH có dạng : CxHyOz
\(x:y:z=0.075:0.2:0.025=3:8:1\)
CTHH đơn giản nhất : C3H8O
Bài 5 :
Tỉ lệ thể tích tương ứng với tỉ lệ số mol nên :
\(V_{CH_4}=a\left(l\right),V_{C_2H_6}=b\left(l\right)\)
\(CH_4+2O_2\underrightarrow{^{^{t^0}}}CO_2+2H_2O\)
\(C_2H_6+\dfrac{7}{2}O_2\underrightarrow{^{^{t^0}}}2CO_2+3H_2O\)
\(V_{hh}=a+b=3.36\left(l\right)\left(1\right)\)
\(V_{CO_2}=a+2b=4.48\left(l\right)\left(2\right)\)
\(\Rightarrow a=2.24,b=1.12\)
\(\%V_{CH_4}=\dfrac{2.24}{3.36}\cdot100\%=66.67\%\)
\(\%V_{C_2H_6}=33.33\%\)
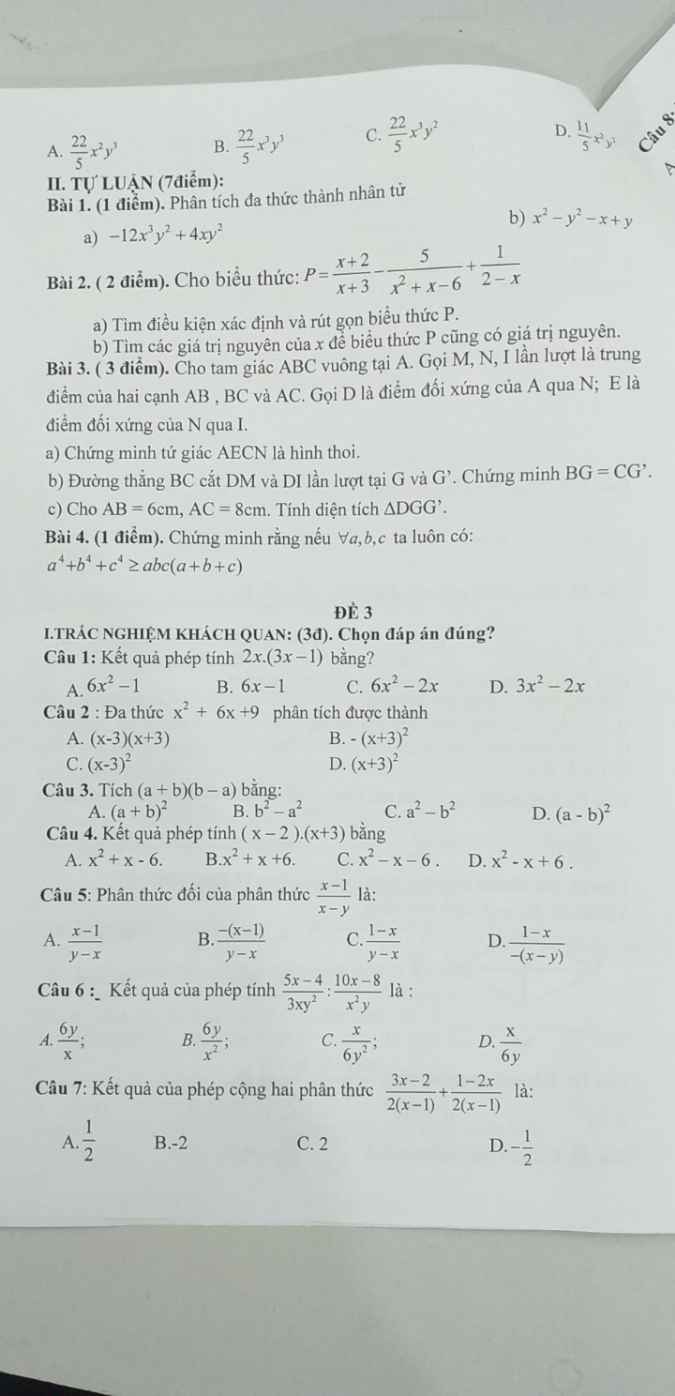
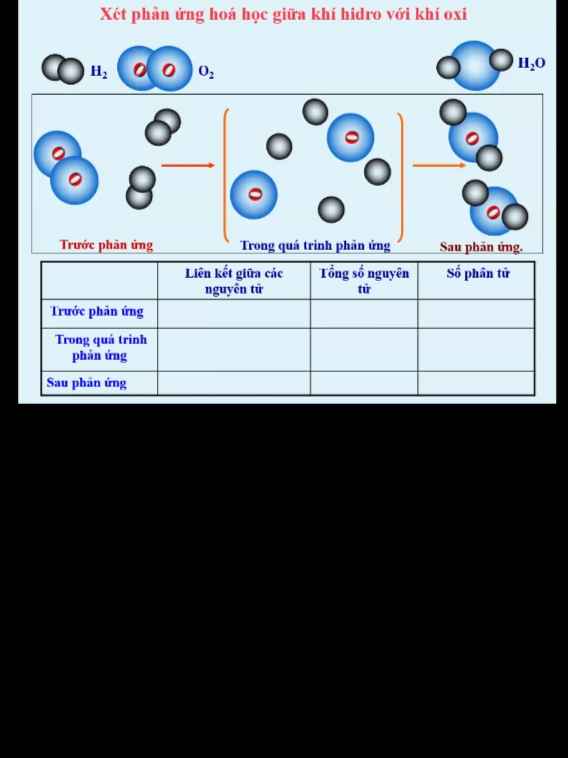

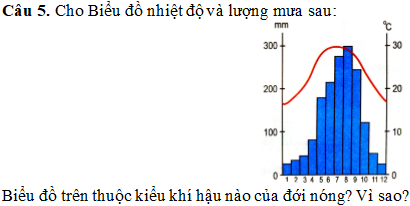

 rồi
rồi 


Bài 4:
\(\left\{{}\begin{matrix}a^4+b^4\ge2a^2b^2\\b^4+c^4\ge2b^2c^2\\c^4+a^4\ge2a^2c^2\end{matrix}\right.\\ \Leftrightarrow2\left(a^4+b^4+c^4\right)\ge2\left(a^2b^2+b^2c^2+c^2a^2\right)\\ \Leftrightarrow a^4+b^4+c^4\ge a^2b^2+b^2c^2+c^2a^2\left(1\right)\\ \left\{{}\begin{matrix}a^2b^2+b^2c^2\ge2ab^2c\\b^2c^2+c^2a^2\ge2abc^2\\c^2a^2+a^2b^2\ge2a^2bc\end{matrix}\right.\\ \Leftrightarrow2\left(a^2b^2+b^2c^2+c^2a^2\right)\ge2\left(a^2bc+ab^2c+abc^2\right)\\ \Leftrightarrow a^2b^2+b^2c^2+c^2a^2\ge a^2bc+ab^2c+abc^2=abc\left(a+b+c\right)\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Dấu \("="\Leftrightarrow a=b=c\)