Cho hình chóp S.ABCD gọi MN lần lượt là trung điểm của AB và BC. G1, G2 là trọng tâm của tam giác SAB, SBC. Chứng minh AC // (SMN)
G1,G2 // (SAC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2018
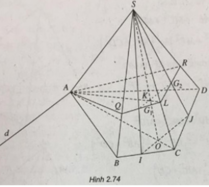
Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có I J / / G 1 G 2 nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi O = IJ ∩ AC, K = G 1 G 2 ∩ S O , L = AK ∩ SC
L G 2 cắt SD tại R
L G 2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.
CM
15 tháng 11 2018
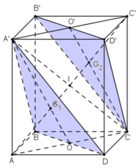
a) + A’D’ // BC và A’D’ = BC
⇒ A’D’CB là hình bình hành
⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)
+ BB’ // DD’ và BB’ = DD’
⇒ BDD’B’ là hình bình hành
⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)
A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)
Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).
b) Gọi O = AC ∩ BD
+ Ta có: O ∈ AC ⊂ (AA’C’C)
⇒ A’O ⊂ (AA’C’C).
Trong (AA’C’C), gọi A’O ∩ AC’ = G1.
G1 ∈ A’O ⊂ (A’BD)
⇒ G1 ∈ AC’ ∩ (BDA’).
+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’
⇒ A’I = IC.
⇒ AI là trung tuyến của ΔA’AC
⇒ G 1 = A ’ O ∩ A C ’ là giao của hai trung tuyến AI và A’O của ΔA’AC
⇒ G 1 là trọng tâm ΔA’AC
⇒ A ’ G 1 = 2 . A ’ O / 3
⇒ G 1 cũng là trọng tâm ΔA’BD.
Vậy AC' đi qua trọng tâm G 1 của ΔA’BD.
Chứng minh tương tự đối với điểm G 2 .
c) *Vì G 1 là trọng tâm của ΔAA’C nên A G 1 / A I = 2 / 3 .
Vì I là trung điểm của AC’ nên AI = 1/2.AC’
Từ các kết quả này, ta có : A G 1 = 1 / 3 . A C ’
*Chứng minh tương tự ta có : C ’ G 2 = 1 / 3 . A C ’
Suy ra : A G 1 = G 1 G 2 = G 2 C ’ = 1 / 3 . A C ’ .
d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.
19 tháng 3 2016
Từ giả thiết suy ra với mọi O đều có ?
\(\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\) và \(\overrightarrow{OG_1}=\frac{1}{3}\left(\overrightarrow{OA}_1+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\)
Mà :
\(\overrightarrow{OG_2=}\frac{1}{3}.\left(\overrightarrow{OGa}+\overrightarrow{OG_b}+\overrightarrow{OG_c}\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB_1}+\overrightarrow{OC_1}\right)+\frac{1}{3}\left(\overrightarrow{OB}+\overrightarrow{OC_1}+\overrightarrow{OA_1}\right)+\frac{1}{3}\left(\overrightarrow{OC}+\overrightarrow{OA_1}+\overrightarrow{OB_1}\right)\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\frac{2}{3}\left(\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\right)\)
\(=\frac{1}{3}\overrightarrow{OG}+\frac{2}{3}\overrightarrow{OG_1}\)
Suy ra :
\(3\overrightarrow{OG_2}=\overrightarrow{OG}+2\overrightarrow{OG_1}\) với mọi O. Điều này có nghĩa là \(G,G_1,G_2\) thẳng hàng => Điều phải chứng minh
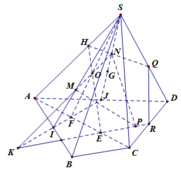
+) Xét △ABC có MN là đường trung bình ⇒MN//AC
Mà MN∈ (SMN) ⇒AC// (SMN)
+) Xét △SMN có \(\dfrac{SG1}{SM}\)=\(\dfrac{SG2}{SN}\)=\(\dfrac{2}{3}\)( Tính chất trọng tâm)
⇒G1G2//MN ⇒ G1G2//AC ( Vì AC//MN)
Mà AC∈(SAC) ⇒ G1G2// (SAC)
cảm ơn nhiều ạ mặc dù e đã nộp bài :">