Cho hình chóp S.ABCD. Hai điểm M và G lần lượt là trọng tâm tam giác SAB và SAD; điểm N thuộc SG và P nằm trong...

PT

Pham Trong Bach

26 tháng 2 2017

Cho hình chóp S.ABCD. Hai điểm M và G lần lượt là trọng tâm tam giác SAB và SAD; điểm N thuộc SG và P nằm trong tứ giác ABCD. Gọi I; J lần lượt là trung điểm của AB và AD và K là giao điểm của MN và IJ; E là giao điểm của KP và AC; F là giao điểm của IJ và AC. Gọi H là giao điểm của OE và SA; Q là giao điểm của NH và SD. Tìm giao tuyến của (MNP ) và (SCD) A. QR trong đó R là giao điểm của KP và CD B. QE...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

26 tháng 2 2017

Đúng(0)

NM

Nguyễn Minh Huy

22 tháng 12 2020 - olm

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD)

c)Tìm giao điểm E của SO và (CGM). Tính tỉ số \(\frac{SE}{SO}\)

#Toán lớp 11

0

N

Ngân

17 tháng 8 2016

giúp mình 2 bài này vs ạ, mình dốt toán hình, đặc biệt là hình không gian. cảm ơn nhìubài 1:trong \(\alpha\) cho tứ giác lồi ABCD, S thuộc (\(\alpha\)). M, N lần lượt là trùg điểm của CD và SD. P thuộc đoạn SB sao cho SP=2PB. hỏi:a: Tìm giao tuyến của SAM và SBD; SAM và SACb: Tìm giao tuyến của AND và ABCDbài 2:cho 4 điểm A,B,C,D không đồng phẳng. M, N lần lượt là trung điểm của AD và BC.a: tìm giao tuyến...

Đọc tiếp

#Toán lớp 11

0

LL

Linh Lê

6 tháng 1 2021

cho hình chóp S.ABCD có đáy ABCD là hình bình hành .Gọi O là giao điểm của AC và BD .M và N lần lượt là trung điểm của CD và SA . G là trọng tâm tam giác SAB .Gọi \(\Delta\) là giao tuyến của 2 mặt phẳng (SAD) và (SMG),P là giao điểm của đường thẳng OG và \(\Delta\) .Chứng minh P,N ,D thẳng hàng

#Toán lớp 11

0

N

Ngân

17 tháng 11 2016

giúp mình giải những bài này vs, mình đg cần gấp, thanks.bài 1: Cho tứ diện ABCD . Gọi G1 và G2 lần lượt là trọng tâm của tam giác ACD và BCD.1. Tìm giao tuyến của hai mặt phẳng (CG1G2) và (ABD).2. Chứng minh rằng G1G2 song song mặt phẳng (ABC).bài 2: cho tứ dện ABCD có G là trọng tâm. Gọi A1 là trọng tâm của tam giác BCDa. CMR: A, G, A1 thẳng hàngb. CMR: GA=3GA'bài 3: cho tứ diện ABCD và 3 điểm P,Q,R lần...

Đọc tiếp

#Toán lớp 11

0

PT

Pham Trong Bach

13 tháng 11 2018

Cho hình chóp S.ABCD. Hai điểm G; H lần lượt là trọng tâm tam giác SAB và SCD. Gọi O là giao điểm của AC và BD; I là giao điểm của SO và GH. Tìm giao tuyến của: (BGH) và (SAC)

A. HI

B .GI

C. KI với K là giao điểm của SA và BG

D. đáp án khác

#Toán lớp 11

1

CM

Cao Minh Tâm

13 tháng 11 2018

Đúng(0)

PN

Phuc Nguyen

16 tháng 8 2016

cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O.Gọi I,J lần lượt là trung điểm BC,SC, K(SD sao cho SK=KD.
a> Cm: OJ//(SAD), OJ//(SAB)
B>CM: OI//(SCD), IJ//(SBD)
C> Gọi M là giao điểm cũa AI và BD. CM MK//(SBC)
cần gấp ạ!

#Toán lớp 11

1

NT

nguyễn thị mai anh

16 tháng 8 2016

bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)

Đúng(0)

PN

Phuc Nguyen

16 tháng 8 2016

thuộc ban nhé. có lẽ mình ghi sai

Đúng(0)

BN

Bình Như

16 tháng 12 2020

Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, AC và P là điểm nằm trên cạnh AB sao choBP = 3AP.a) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBC).b) Gọi E, F là hai điểm nằm trong hai tam giác SAD và SBC. Tìm giao điểm củađường thẳng EF với mặt phẳng (MNP).

cứu mình với mai thi rồi :((

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

17 tháng 12 2020

a.

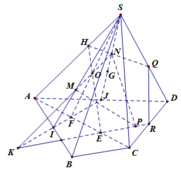
Trong mp (SAB) nối PM kéo dài cắt SB tại G

Trong mp (ABCD) nối PN cắt BC kéo dài tại H

\(\Rightarrow GH=\left(MNP\right)\cap\left(SBC\right)\)

b.

Nối SE cắt AD tại I, nối SF cắt BC tại K

Trong mp (ABCD), nối IK cắt PN kéo dài tại S

Trong mp (SBC), SF kéo dài cắt GH tại R

\(\Rightarrow RS\) là giao tuyến của (MNP) và (SEF)

Trong mp (SEF), nối RS và EF cắt nhau tại Q

\(\Rightarrow Q=EF\cap\left(MNP\right)\)

Đúng(1)

NM

NGUYỄN MINH HUY

22 tháng 12 2020

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD)

c)Tìm giao điểm E của SO và (CGM). Tính tỉ số \(\frac{SE}{SO}\)

#Toán lớp 11

1

HT

Hoàng Tử Hà

22 tháng 12 2020

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v

undefined

Đúng(1)

NM

NGUYỄN MINH HUY

23 tháng 12 2020

cảm ơn bạn nha

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP