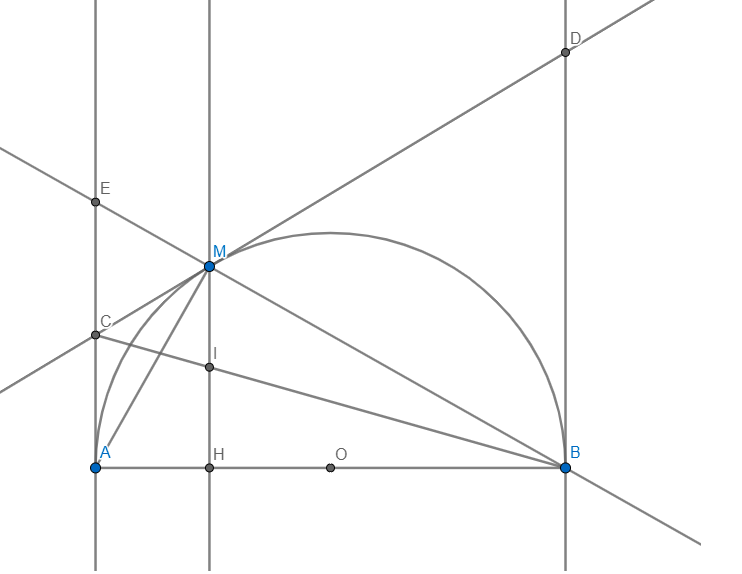
Bài 3(3 điểm). Cho nửa đường tròn tâm O đường kính AB = 2R, M là điểm bất kì trên nửa đường tròn (M ne A,B) . Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn, về các tiếp tuyến Ax và By với nửa đường tròn. Qua M kẻ tiếp tuyến thứ ba với nửa đường tròn, tiếp tuyến này cắt Ax, By lần lượt tại C và D. a, Chứng minh rằng: CD = AC + BD và góc COD = 90 b, Chứng minh rằng: AC.BD=R^ 2 c. Gọi K là giao điểm của AD và BC. Chứng minh rằng: MK vuông góc với AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
góc DMO+góc DBO=180 độ
=>DMOB nội tiếp
b: Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc DOC=1/2*180=90 độ
Xét ΔDOC vuông tại O có OM là đường cao
nên CM*MD=OM^2
=>AC*BD=R^2

c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF

b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB


a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DB là tiếp tuyến
DM là tiếp tuyến
Do đó: DB=DM
Ta có: MC+MD=DC
nên DC=CA+DB