Mọi người ơi, có ai biết vẽ lại tranh của chị Huta Chan không ạ? Giúp mình với, đứa bạn cứ đòi mình vẽ ấy, mà mình có biết vẽ đâu!!😢😢
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Thí nghiệm: Cho một ít KMnO4 hoặc KClO3 vào ống nghiệm có cắm ống dẫn khí,đầu ống nghiệm được nút lại.
Câu hỏi là: cách điều chế oxi trong phòng thí nghiệm á
Giúp mình đi mọi ngừi ơiii 😥🥺

Bài 2:
a: \(201^3=8120601\)
b: \(199^3=7880599\)
c: \(52^3-8=140600\)
d: \(23^3-27=12140\)
e: \(99^3=970299\)
f: \(62\cdot58=3596\)
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: \(\left(5x+5\right)^2+10\cdot\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left(5x+5\right)^2+2\cdot\left(5x+5\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(6x+2\right)^2\)
\(=36x^2+24x+4\)
c: \(\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=x^3-3x^2y+3xy^2-y^3+3x^2y-3xy^2\)
\(=x^3-y^3\)
d: \(\left(1-2x\right)\left(1+2x+4x^2\right)+8\left(x-1\right)\left(x^2+x+1\right)\)
\(=1-8x^3+8\left(x^3-1\right)\)
\(=1-8x^3+8x^3-8\)
=-7

a: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
b: Ta có: ΔBAK=ΔBDK
nên KA=KD
mà BA=BD
nên BK là đường trung trực của AD
a)Xét \(\Delta BAK\) và \(\Delta BDK\) có:
AB=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
=> \(\Delta BAK\) = \(\Delta BDK\) (c-g-c)
b)Gọi O là giao điểm của AD và BK
Xét \(\Delta ABO\) và \(\Delta DBO\) có :
BO chung
\(\widehat{ABO}=\widehat{DBO}\)
AB=DB
=> \(\Delta ABO\) và \(\Delta DBO\) (c-g-c)
=> AO=BO (1) ; \(\widehat{AOB}=\widehat{DOB}\)
Có : \(\widehat{AOB}+\widehat{DOB}=180^o\) mà \(\widehat{AOB}=\widehat{DOB}\)
=> \(\widehat{AOB}=\widehat{DOB}=\dfrac{180^o}{2}=90^o\) (2)
Từ (1)(2) => BK là đường trung trực cùa AD

Ta có : \(12a+7b=64\)
Do \(64⋮4,12a⋮4\) \(\Rightarrow7b⋮4\) mà \(\left(7,4\right)=1\)
\(\Rightarrow b⋮4\) (1)
Từ giả thiết \(\Rightarrow7b\le64\) \(\Leftrightarrow b\le9\) kết hợp với (1)
\(\Rightarrow b\in\left\{4,8\right\}\)
+) Với \(b=4\) thì : \(12a+7\cdot4=64\)
\(\Leftrightarrow12a=36\)
\(\Leftrightarrow a=3\) ( thỏa mãn )
+) Với \(b=8\) thì \(12a+7\cdot8=64\)
\(\Leftrightarrow12a=8\)
\(\Leftrightarrow a=\frac{8}{12}\) ( loại )
Vậy : \(\left(a,b\right)=\left(3,4\right)\)

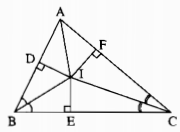
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
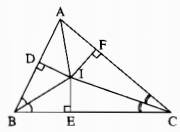
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W



mik ko bt vẽ