cho nửa đường tròn (O) có đường kính AB và điểm C thuộc nửa đường tròn đó (C khác A,B).Lấy điểm M thuộc dây BC(M khác B,C) .Tia AM cắt cung nhỏ BC tại điểm N,tia AC cắt BN tại điểm P.Cm:PCMN là tứ giác nội tiếp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
Xét tứ giác FCDE có
\(\widehat{FCD}+\widehat{FED}=180^0\)
Do đó: FCDE là tứ giác nội tiếp
b: Xét ΔACD vuông tại C và ΔBED vuông tại E có
\(\widehat{CDA}=\widehat{EDB}\)
Do đó: ΔACD\(\sim\)ΔBED
Suy ra: DA/DB=DC/DE
hay \(DA\cdot DE=DB\cdot DC\)

a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC

a: góc ACB=1/2*sđ cung AB=90 độ
=>góc FCD=90 độ
góc AEB=1/2*sđ cung AB=90 độ
=>góc FED=90 độ
=>góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔCAD vuông tại C và ΔCBF vuông tại C có
góc CAD=góc CBF
=>ΔCAD đồng dạng với ΔCBF
=>CA/CB=CD/CF
=>CA*CF=CB*CD

a: góc ACB=1/2*sđ cung AB=90 độ
=>góc FCD=90 độ
góc AEB=1/2*sđ cung AB=90 độ
=>góc FED=90 độ
=>góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔCAD vuông tại C và ΔCBF vuông tại C có
góc CAD=góc CBF
=>ΔCAD đồng dạng với ΔCBF
=>CA/CB=CD/CF
=>CA*CF=CB*CD

a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC

a/ Tam giác ABC nội tiếp đường tròn (O) có cạnh AB là đường kính của đường tròn (O)
=> Tam giác ABC vuông tại C
=> Góc ACB=90 độ (1)
Mà: góc ACB+góc DCF=180 độ (kề bù ) (A,C,F thẳng hàng) (2)
Từ (1) và (2)=>góc DCF=90 độ (3)
Tam giác AEB nội tiếp đường tròn (O) có cạnh AB là đường kính của đường tròn (O)
=> Tam giác AEB vuông tại E
=> góc AEB=90 độ (4)
Mà: góc AEB+góc DEF =180 độ (kề bù) (B,E,F thẳng hàng) (5)
Từ(4) và (5)=>góc DEF=90 độ (6)
Từ (3) và (6)=> góc DCF+góc DEF=180 độ
=> Tứ giác FCDE nội tiếp (đpcm)
b/Xét hai tam giác: tam giác ADC và tam giác BED có:
góc ADC= góc BED (đối đỉnh)
góc ACB= goc AEB (=90 độ theo c/m câu a)
hay góc ACD= góc BED ( C,D,B thẳng hàng và A,D,E thẳng hàng)
Do đó, tam giác ADC đồng dạng với tam giác BED (g.g)
=> DA/DB=DC/DE
<=> DA.DE=DB.DC (đpcm)

https://hoidap247.com/cau-hoi/296770 cậu vào link này xem bài tham khảo rồi tự làm hộ mk nha, mk bận quá nên k có thời gian giải cả bài ra chi tiết cho Vy đc, thông cảm giùm mk với ạ, thanks ^6
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC

a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)
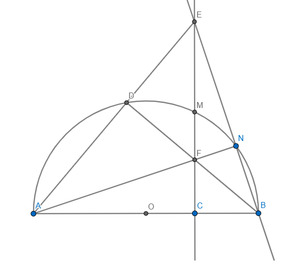
Xét ΔABC có AB là đườn kính đường tròn ngoại tiếp tam giác
=> ΔABC vuông tại C hay AP ⊥ BC
CMTT => AN ⊥ BP
Xét tứ giác PCMN có: \(\widehat{PCM}+\widehat{PNM}=90^o+90^o=180^o\)
=> PCMN là tứ giác nội tiếp
có hình ko bạn:<