Cho góc xOy nhọn Oz là tia phân giác của góc xOy . Trên Ox lấy điểm M , N sao cho OM < ON . Trên Oy lấy điểm P , Q sao cho OP = OM , OQ = ON giao điểm MQ và NP tại E . Chứng minh rằng :
a) tam giác NOP = tam giác QOM
b) tam giác EMN = tam giác EPQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMOP và ΔNOP có
OM=ON
\(\widehat{MOP}=\widehat{NOP}\)
OP chung
Do đó: ΔMOP=ΔNOP
b: Ta có: ΔMOP=ΔNOP
Suy ra: PM=PN
hay P là trung điểm của MN
c: Ta có: OM=ON
nên O nằm trên đường trung trực của MN(1)
Ta có: P là trung điểm của MN
nên P nằm trên đường trung trực của MN(2)
từ (1) và (2) suy ra OP là đường trung trực của MN
hay OP\(\perp\)MN

#\(N\)
`a,` Xét Tam giác `OMP` và Tam giác `ONP` có:
`OM = ON (g``t)`
\(\widehat{MOP}=\widehat{NOP}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OP` chung
`=>` Tam giác `OMP =` Tam giác `ONP (c-g-c)`
`b,` Vì Tam giác `OMP =` Tam giác `ONP (a)`
`=> MP = NP (` 2 cạnh tương ứng `)`
`=>`\(\widehat{MPH}=\widehat{NPH}\) `(` 2 góc tương ứng `)`
Xét Tam giác `MPH` và Tam giác `NPH` có:
`MP = NP (CMT)`
\(\widehat{MPH}=\widehat{NPH}(CMT)\)
`PH` chung
`=>` Tam giác `MPH = `Tam giác `NPH (c-g-c)`
`=>`\(\widehat{MHP}=\widehat{NHP}\) `(` 2 góc tương ứng `)`
Mà `2` góc này ở vị trí kề bù
`=>`\(\widehat{MHP}+\widehat{NHP}=180^0\)
`=>` \(\widehat{MHP}=\widehat{NHP}=\)\(\dfrac{180}{2}=90^0\)
`=>`\(MN\perp OP\left(đpcm\right)\)
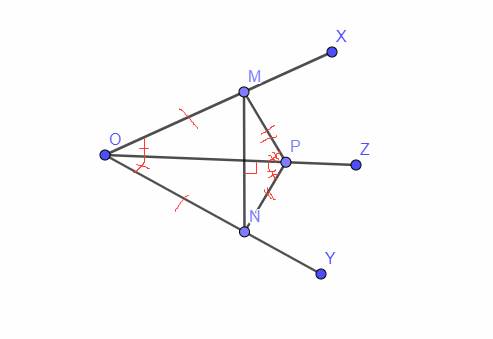

tự vẽ hình
a) Tam giác MOQ và PON có: OM=OP ; OQ =ON ; góc O chung => tgiac MOQ=PON (c-g-c)
=> MQ = PN
b) Theo a) => Góc Q = N (1)
góc OPN = OMQ => IPQ = IMN ( cùng bù với 2 góc bằng nhau) (2)
Mặt khác ON -OM =OQ -OP => PQ =MN (3)
1;2;3 => Tam giác IMN = IPQ (g-c-g) => IM =IP ; IN =IQ
c) theo b) => IM = IP => tam giác OIM = OIP ( c-c-c)=> Góc MOI =POI hay OI là phân giác xOy
d) vì OP = OM và IP =IM => OI là đường trung trực của MP
e) tương tự d) => OI là trung trực NQ => OI vuông góc NQ ; OI vuông góc với MP => NQ // MP

a: Xét ΔOMF và ΔOEN có
OM=OE
\(\widehat{O}\) chung
OF=ON
Do đó: ΔOMF=ΔOEN
Suy ra: MF=EN

Xét ΔOQM và ΔOPN có
OQ=OP
góc O chung
OM=ON
=>ΔOQM=ΔOPN
=>góc OQM=góc OPN
a) ta có \(OP+PQ=OQ\)
\(OM+MN=ON\)
mà \(OP=OM;PQ=MN\)
\(\Rightarrow OQ=ON\)
Xét \(\Delta NOPvà\Delta QOMcó\)
\(OP=OM\) ( giả thiết )
\(\widehat{QON}\) là góc chung
\(OQ=ON\) (chứng minh trên)
\(\Rightarrow\Delta NOP=\Delta QOM\left(c-g-c\right)\)
vậy \(\Delta NOP=\Delta QOM\)
b) tự làm nhé