Bài 1 . Viết thuật toán tính diện tích hình tròn bán kính r (nêu ý tưởng ; xác định bài toán ; dùng cả liệt kê + sơ đồ khối)
Bài 2 . Viết thuật toán tính chu vi hình vuông cạnh a (nêu ý tưởng ; xác định bài toán ; dùng cả liệt kê + sơ đồ khối)
Bài 3 . Các loại bộ nhớ ngoài thường dùng hiện nay là những loại nào? Cho biết điểm khác nhau giữa chúng

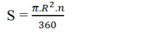
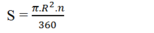
Bài 1:
Ý tưởng: Sau khi nhập bán kính r, chúng ta sẽ tính diện tích theo công thức \(S=r^2\cdot pi\)
Xác định bài toán
-Input: Bán kính r
-Output: Diện tích hình tròn có bán kính r
Mô tả thuật toán
-Bước 1: Nhập r
-Bước 2: \(s\leftarrow pi\cdot sqr\left(r\right)\)
-Bước 3: Xuất s
-Bước 4: Kết thúc
Bài 2:
Ý tưởng: Sau khi nhập cạnh a chúng ta sẽ tính chu vi hình vuông có cạnh a theo công thức \(S=4\cdot a\)
Xác định bài toán:
-Input: Cạnh a
-Output: Chu vi hình vuông có cạnh a
Mô tả thuật toán
-Bước 1: Nhập a
-Bước 2: s←a*4;
-Bước 3: Xuất s
-Bước 4: Kết thúc