Cho hình chóp S.ABCD có tất cả các cạnh bằng a, đáy ABCD là hình bình hành.Gọi M,N lần lượt là trung điểm AB,SC.
a) Tìm thiết diện tạo bởi mặt phẳng (ABN) và hình chóp.Tính diện tích thiết diện
b) Chứng minh đường thẳng BN // (SMD).
c)Xác định các điểm I,J lần lượt là giao điểm của đường thẳng AN và đường thẳng MN với mặt phẳng (SBD). Chứng minh I,J,K thẳng hàng

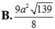
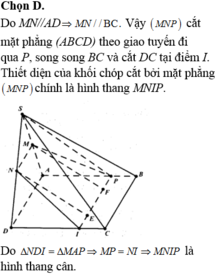

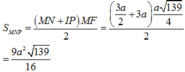


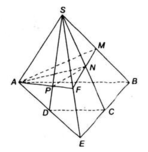

Gọi O là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC=SD\Rightarrow OA=OB=OC=OD\)
\(\Rightarrow ABCD\) là hình vuông
Gọi P là trung điểm SD \(\Rightarrow NP//CD\Rightarrow NP//AB\)
\(\Rightarrow ABNP\) là thiết diện của (ABN) và chóp
\(NP=\dfrac{1}{2}CD=\dfrac{a}{2}\)
\(AP=\dfrac{a\sqrt{3}}{2}\) (trung tuyến trong tam giác đều cạnh a)
Gọi H là chân đường cao hạ từ P xuống AB, do ABNP là hình thang cân nên:
\(PH=\sqrt{AP^2-\left(\dfrac{AB-NP}{2}\right)^2}=\dfrac{a\sqrt{11}}{4}\)
\(S_{ABNP}=\dfrac{1}{2}.PH.\left(NP+AB\right)=...\)
Nối dài DM cắt BC kéo dài tại E
Theo talet: \(\dfrac{EB}{EC}=\dfrac{BM}{CD}=\dfrac{1}{2}\Rightarrow\) B là trung điểm EC
\(\Rightarrow BN\) là đường trung bình tam giác SEC \(\Rightarrow BN//SE\Rightarrow BN//\left(SMD\right)\)
Ở câu c, K là điểm nào vậy bạn?
Cách xác định I; J:
Trong mp (SAC), nối AN cắt SO tại I
Trong mp (ABCD), nối CM cắt BD tại R
Trong mp (SMC), nối MN cắt SR tại J