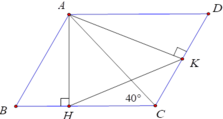
Cho hình bình hành ABCD,góc A lớn hơn 90 độ,đường cao AH và AK.CMR: góc AKH=góc ACH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2018
+/ Vì AH là đường cao ứng với đáy CD của hbh ABCD (gt) => Diện tích hbh ABCD=AH.CD (1)
Vì AK là đường cao ứng với đáy BC của hbh ABCD (gt) => Diện tích hbh ABCD=AK.BC (2)
Từ (1) và (2)=> AH.CD=AK.BC <=> AH/BC = AK/CD
Vì ABCD là hbh (gt)=> AB=CD (t/c hbh)
=> AH/BC=AK/AB
+/ Vì ABCD là hbh (gt)=> AB//CD (t/c hbh)
Mà AH vuông góc CD (gt)
=> AH vuông góc AB (định lí từ vuông góc đến song song)=> góc HAB=90o <=> góc KAH + góc BAK= 90o
Vì AK vuông góc BC (gt) => tam giác ABK vuông ở K có góc BAC + góc ABC= 90o (2 góc phụ nhau)
=> góc KAH = góc ABC (cùng phụ góc BAK)
+/ Xét tam giác KAH và tam giác ABC có:
- AH/BC=AK/AB (cmt)
- góc KAH=góc ABC (cmt)
=> tam giác KAH đồng dạng tam giác ABC (c.g.c)
<=> góc AKH = góc BAC (khái niệm về tam giác đồng dạng)
Mà AB//CD (cmt)=> góc BAC=góc ACH (2 góc so le trong)
=> góc AKH= góc ACH (cùng bằng góc BAC) (đpcm)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 3 2021
a/ Xét tg vuông AHD và tg vuông AKB có
\(\widehat{BAK}+\widehat{ABC}=90^o\)
\(\widehat{DAH}+\widehat{ADC}=90^o\)
Mà \(\widehat{ABC}=\widehat{ADC}\) (Hai góc đối của hbh)
\(\Rightarrow\widehat{DAH}=\widehat{BAK}\)
=> tg AHD đồng dạng với tg AKB \(\Rightarrow\frac{AH}{AK}=\frac{DA}{AB}\) mà AB = DC (hai cạnh đối của hbh) \(\Rightarrow\frac{AH}{AK}=\frac{DA}{DC}\left(dpcm\right)\)
b/ Ta có K và H đều nhìn AC dưới 1 góc 90 độ
=> Tứ giác AKCH là tứ giác nội tiếp đường tròn đường kính AC
=> sđ \(\widehat{AKH}\) = sđ \(\widehat{ACH}\) = 1/2 sđ cung AH (Góc nội tiếp đường tròn) \(\Rightarrow\widehat{AKH}=\widehat{ACH}\left(dpcm\right)\)
D
27 tháng 1 2022
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
HB
0
CM
19 tháng 1 2018
Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B