Cho hình chóp S.ABCD có ABCD là hình bình hành tâm O. Gọi K là trung điểm của SC. Chứng minh rằng : KO // ( SAB).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2023
Để chứng minh a. ON//(SAB) và b. (OMN)//(SCD), chúng ta có thể sử dụng các định lý và quy tắc trong hình học không gian.
a. Để chứng minh ON//(SAB), ta có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Theo định lý này, nếu có hai đường thẳng cắt một mặt phẳng và các đường thẳng này đều song song với một đường thẳng thứ ba trong mặt phẳng đó, thì hai đường thẳng đó cũng song song với nhau. Áp dụng định lý này, ta có thể chứng minh ON//(SAB) bằng cách chứng minh rằng ON và AB đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.
b. Để chứng minh (OMN)//(SCD), ta cũng có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Tương tự như trường hợp trước, ta cần chứng minh rằng OM và CD đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.
Tuy nhiên, để chứng minh chính xác các phần a và b, cần có thêm thông tin về các góc và độ dài trong hình chóp S.ABCD.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 12 2021
a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)
25 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)
1 tháng 11 2023
a: XétΔSDB có
M,O lần lượt là trung điểm của DS,DB
=>MO là đường trung bình của ΔSDB
=>MO//SB
SB//MO
MO\(\subset\)(MAC)
SB không nằm trong mp(MAC)
Do đó: SB//(MAC)
b: Xét (OMA) và (SAB) có
\(A\in\left(OMA\right)\cap\left(SAB\right)\)
OM//SB
Do đó: (OMA) giao (SAB)=xy,xy đi qua A và xy//OM//SB
8 tháng 11 2023
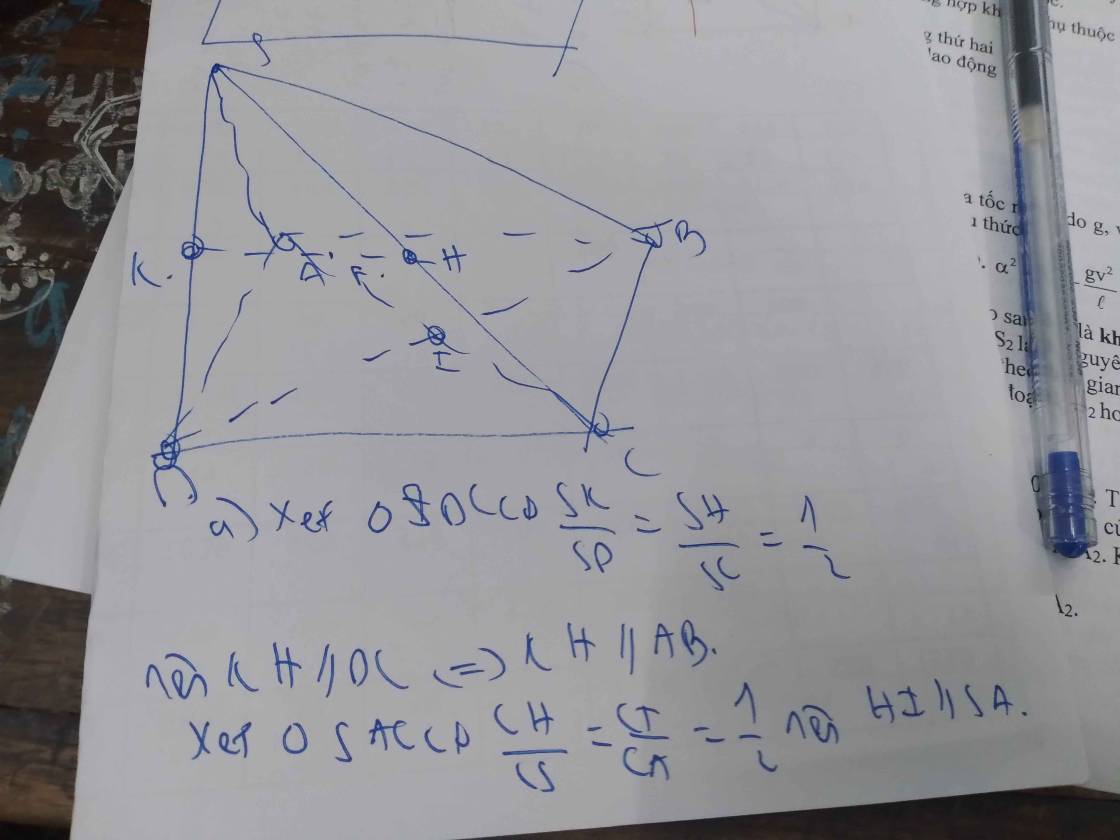
a: XétΔCAS có
I,H lần lượt là trung điểm của CA,CS
=>IH là đường trung bình
=>IH//SA
mà \(SA\subset\left(SAB\right)\); IH không thuộc mp(SAB)
nên IH//(SAB)
Xét ΔSCD có
H,K lần lượt là trung điểm của SC,SD
=>HK là đường trung bình của ΔSCD
=>HK//CD
mà CD//AB
nên HK//AB
mà \(AB\subset\left(SAB\right)\) và HK không thuộc mp(SAB)
nên HK//(SAB)
HK//(SAB)
IH//(SAB)
\(HK,IH\subset\left(HIK\right)\)
Do đó: (HIK)//(SAB)
b: HK//CD
\(CD\subset\left(ABCD\right)\)
HK không thuộc mp(ABCD)
Do đó; HK//(ABCD)
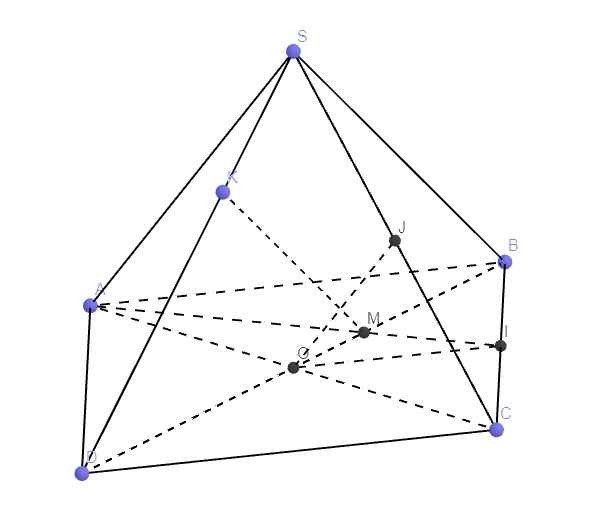
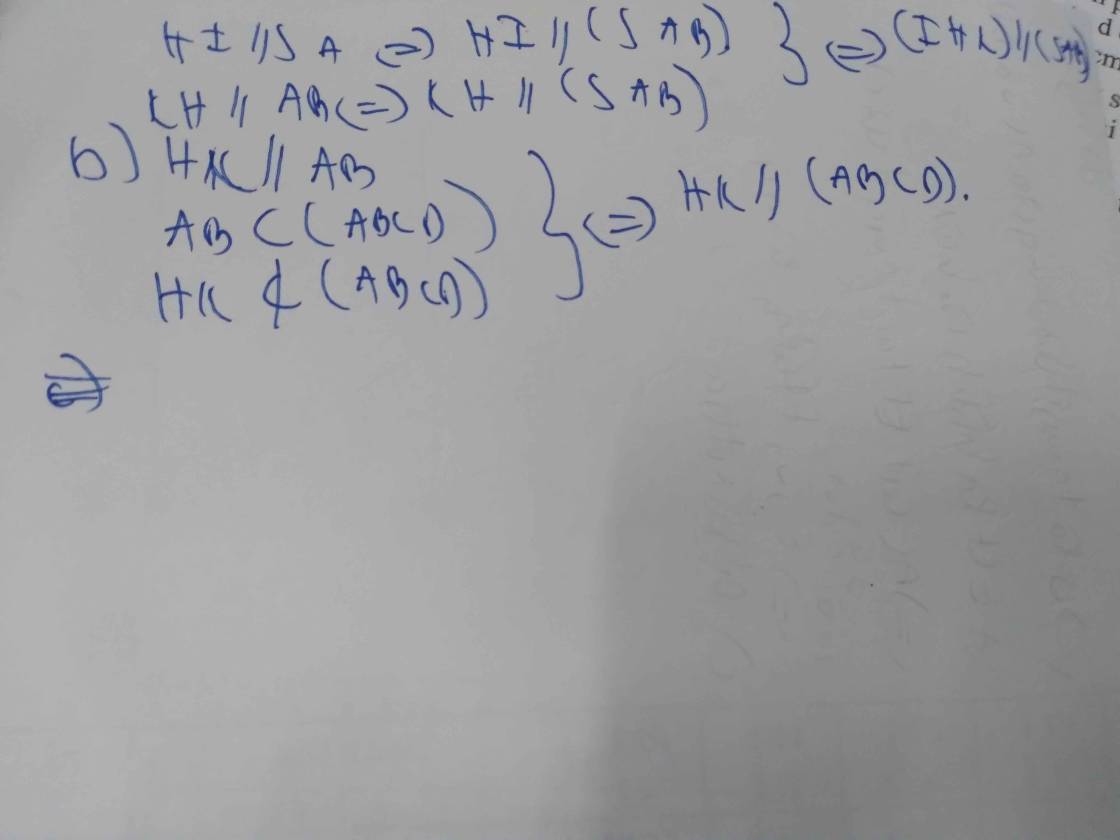
Lời giải:
Vì $ABCD$ là hình bình hành nên tâm $O$ là trung điểm $AC$
$\Rightarrow OK$ là đường trung bình của $SAC$ ứng với cạnh $SA$
$\Rightarrow OK\parallel SA$
Mà $SA\subset (SAB)$ nên $OK\parallel (SAB)$