Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 4 ; 5 ; B 3 ; 4 ; 0 ; C 2 ; − 1 ; 0 và mặt phẳng P : 3 x − 3 y − 2 z − 12 = 0. Gọi M a ; b ; c thuộc (P) sao cho M A 2 + M B 2 + 3 M C 2 đạt giá trị nhỏ nhất. Tính tổng a + b + c
A. 3
B. 2
C. - 2
D. - 3




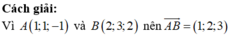
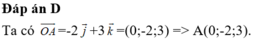
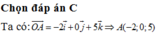
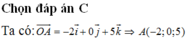
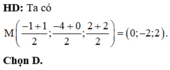
Đáp án A
P = M I 2 +2 M I → . I A → +IA 2 + M I 2 +2 M I → . I B → +IB 2 +3MI 2 + 6 M I → . I C → + 3 I C 2
P = 5 M I 2 + IA 2 +IB 2 + 3 I C 2 ⏟ c o n s t + 2 M I → . I A → + I B → + 3 I C → ⏟ 0 →
⇒ P min ⇔ M I min