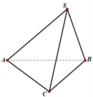
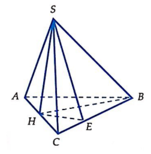
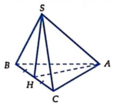
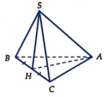
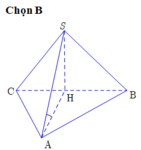
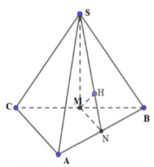
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , A B C ^ = 30 ° , tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).
A. h = 2 a 39 13
B. h = a 39 13
C. h = a 39 26
D. h = a 39 52


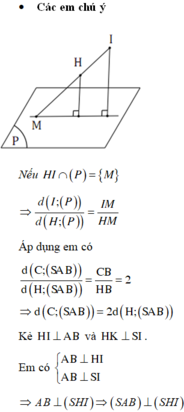

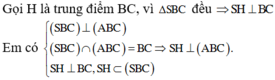


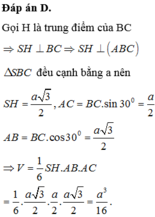
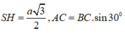
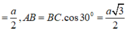
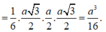

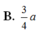
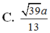
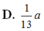



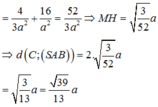

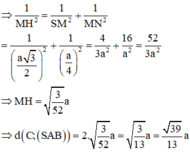
Đáp án B.
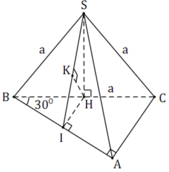
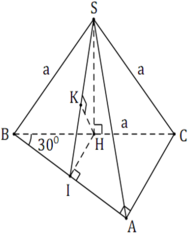
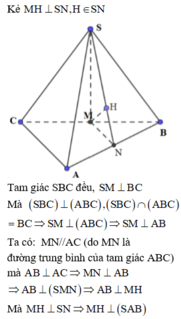
Gọi H là trung điểm của BC khi đó S H ⊥ B C do S B C ⊥ A B C ⇒ S H ⊥ A B C
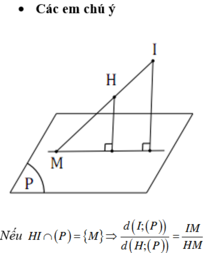
Lại có: C B = 2 C H ⇒ d C ; S A B = 2 d H ; S A B
Dựng H E ⊥ A B H F ⊥ S E ⇒ d H = H F
Mặt khác H E = A C 2 = 1 2 B C . sin A B C ^ = a 4 ; S H = a 3 2
Do đó H F = S H . H E S H 2 + H E 2 = a 39 26 ⇒ d c = a 39 13