Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x 4 - 2 m x 2 + 2 m + m 4 có 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 2 lần bán kính đường tròn nội tiếp?
A. m = 1
B. m = 3 3
C. m = 3 3 2
D. m = 6 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
![]() TXĐ: D = R.
TXĐ: D = R.
![]()
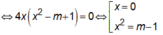
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt ⇔ m -1 > 0 ⇔ m > 1(*)
3 điểm cực trị của đồ thị hàm số là: A(0;1),
Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
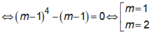
Kết hợp với điều kiện (*) => m = 2
Làm theo bào toán trắc nghiệm như sau:
Hàm số đã cho có 3 điểm cực trị khi ab < 0 ![]()
Chỉ có đáp án D thỏa mãn.

Chọn C
Ta có
![]()
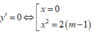 nên hàm số có 3 điểm cực trị khi m > 1.
nên hàm số có 3 điểm cực trị khi m > 1.
Với đk m > 1 đồ thị hàm số có 3 điểm cực trị là:
![]()
![]()
Ta có:
![]()
![]()
Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:
![]()
![]()
![]()
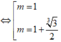
So sánh với điều kiện ta có: m = 1 + 3 3 2 thỏa mãn.
[Phương pháp trắc nghiệm]
Yêu cầu bài toán
![]()
![]()
![]()

Đáp án C

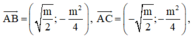
Tam giác ABC cân tại A, do đó để tam giác ABC vuông cân
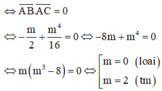

Đáp án D
Ta có y ' = 4 x 3 − 4 m x = 4 x x 2 − m .
Hàm số có 3 điểm cực trị ⇔ y ' = 0 có 3 nghiệm phân biệt, suy ra m > 0 1 .
Suy ra tọa độ 3 điểm cực trị của đồ thị hàm số là
A 0 ; 0 , B m ; − m 2 , C − m ; − m 2 ⇒ A B ¯ = m ; − m 2 A C ¯ = − m ; − m 2 B C ¯ = 2 m ; 0 .
Suy ra tam giác ABC cân tại A.
Gọi H 0 ; − m 2 là trung điểm của B C ⇒ A H ¯ = 0 ; − m 2 ⇒ A H = m 2 .
Suy ra S A B C = 1 2 A H . B C = 1 2 m 2 2 m 2 = m 4 < 1 ⇔ − 1 < m < 1 2 .
Từ (1), (2) ⇒ 0 < m < 1.
Đáp án B
Ta có y ' = 4 x 3 - 4 m x = 4 x ( x 2 - m ) để tồn tại ba điểm cực trị thì m>0 khi đó tọa độ ba điểm cực trị là A ( 0 ; m 4 + 2 m ) , B ( m ; m 4 - m 2 + 2 m ) , C ( - m ; m 4 - m 2 + 2 m )
⇒ A B = A C = m 4 + m , B C = 2 m gọi M là trung điểm B C ⇒ M B = m ⇒ A M = A B 2 - M B 2 = m 4 + m - m = m 2 ⇒ S A B C = 1 2 A M . B C = 1 2 m 2 . 2 m = m 2 . m
Mặt khác r = S P = m 2 m m 4 + m + m = m 2 m 3 + 1 + 1 = m 3 + 1 - 1 m R = A B . A C . B C 4 S = ( m 4 + m ) 2 m 4 m 2 m = 1 2 m 3 + 1 m theo giả thiết R = 2 r ⇒ 1 2 ( m 3 + 1 ) m = 2 ( m 3 + 1 - 1 ) m ⇔ ( m 3 + 1 ) = 4 m 3 + 1 - 4 ⇔ ( m 3 + 1 - 2 ) 2 = 0 ⇔ m 3 + 1 = 2 ⇔ m 3 = 3 ⇔ m = 3 3