1 cây tre cao 9 mét, bị gãy ngang thân, ngọn cay chạm đất, cách gốc 3 mét. hỏi điểm gãy cách gốc bao nhiêu mét ???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

DT
Đỗ Thanh Hải
CTVVIP
7 tháng 3 2021
Gọi chiều dài phần trên gãy ngang là c
Áp dụng định lí Py-ta-go ta được: 52 + 122 = c2
=> c2 = 169 => c = 13m
Cây cột điện dài : 13 + 5 = 18m

20 tháng 10 2021
Điểm gãy cách gốc \(\sqrt{8^2+3,5^2}=\dfrac{\sqrt{305}}{2}\approx8,73\left(m\right)\)

20 tháng 2 2022
Điểm gãy cách gốc:
\(\sqrt{8^2-4^2}=4\sqrt{3}\left(m\right)\)

CM
25 tháng 4 2018
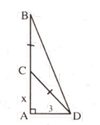
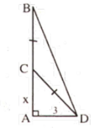
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
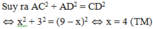
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C

CM
16 tháng 2 2018

Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x CB = CD = 8 – x.
Vì ∆ ACD vuông tại A
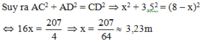
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B
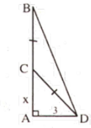


Bài 77 sách bài tập nâng cao và một số chuyên đề, về tự đọc nhé, bn sẽ hiểu hơn đó
mk k có sách đó nhưng mk lm xog rùi