Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo có độ cứng 40 N/m đang dao động điều hòa với biên độ 5 cm. Khi vật đi qua vị trí có li độ 3 cm, con lắc có động năng bằng:
A. 0,024 J
B. 0,032 J
C. 0,018 J
D. 0,050 J
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cơ năng của con lắc là \(W = {{\rm{W}}_d} + {{\rm{W}}_t} \to {{\rm{W}}_d} = {\rm{W}} - {{\rm{W}}_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2} = \dfrac{1}{2}.40\left( {0,{{05}^2} - 0,{{03}^2}} \right) = 0,032 J\).

Đáp án B
Phương pháp: Áp dụng định luật bảo toàn năng lượng
Cách giải:
Áp dụng định luật bảo toàn năng lượng ta có
![]()
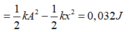

Đáp án B
Động năng tại x=3cm bằng cơ năng trừ thế năng: W d = W - W t = 1 2 k ( A 2 - x 2 ) = 0 , 032 J

Đáp án C
+ Độ biến dạng của lò xo tại vị trí cân bằng ∆ l 0 = m g k = 2 , 5 c m
Với gốc tọa độ tại vị trí cân bằng, vị trí lò xo có lực đàn hồi cực tiểu (lò xo không biến dạng) ứng với
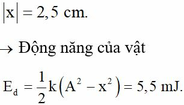
Đáp án B
Động năng: W d = W − W t = 1 2 k A 2 − 1 2 k x 2 = 1 2 k A 2 − x 2 = 0 , 032 J