Trong không gian Oxyz cho A 1 ; − 1 ; 2 , B − 2 ; 0 ; 3 , C 0 ; 1 ; − 2 . M a ; b ; c là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức S = M A → . M B → + 2 M B → . M C → + 3 M C → . M A → đạt giá trị nhỏ nhất. Khi đó T = 12 a + 12 b + c có giá trị là
A. -1
B. 3
C. -3
D. 1


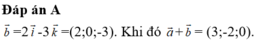
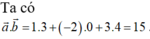
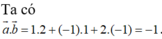
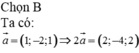
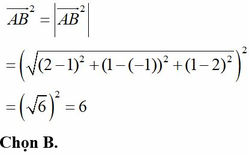
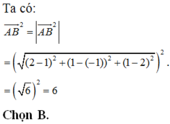
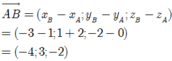
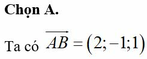
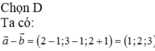
Đáp án A
Gọi I là điểm sao cho 4 I A → + 3 I B → + 5 I C → = 0 → ⇒ I − 1 6 ; 1 12 ; 1 3
M A → . M B → + 2 M B → . M C → + 3 M C → . M A → = I A → − I M → I B → − I M → + 2 I B → − I M → I C → − I M → + 3 I C → − I M → I A → − I M → = I A → . I B → + 2 I B → . I C → + 3 I C → . I A → − I M → 4 I A → + 3 I B → + 5 I C → + 6 I M 2
Do I A → . I B → + 2 I B → . I C → + 3 I C → . I A → là hằng số và I M → 4 I A → + 3 I B → + 5 I C → = 0 Nên S min k h i I M min ⇔ M là hình chiếu của I lên mặt phẳng O x y ⇒ M − 1 6 ; 1 12 ; 0 ⇒ T = − 2 + 1 = − 1