Tìm tất cả các giá trị của tham số m để hàm số y = 3 2 x 4 - 2 m x 2 + 7 3 có cực tiểu mà không có cực đại
A. m ≥ 0
B. m ≤ 0
C. m ≥ 1
D. m = -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2021
Với \(m=-1\) thỏa mãn
Với \(m\ne-1\) hàm chỉ có cực tiểu mà không có cực đại khi:
\(\left\{{}\begin{matrix}m+1>0\\-m\left(m+1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow-1< m\le0\)
Vậy \(-1\le m\le0\)
CM
1 tháng 11 2017
Chọn B
[Phương pháp tự luận]
y ' = 4 ( m - 1 ) x 3 - 6 m x = 0 (*)
TH1 : Nếu m = 1 , (*) trở thành : y ' = - 6 x = 0 hay x= 0 , y ' ' = - 6 < 0
Vậy m = 1 hàm số đạt cực đại tại x = 0
TH2 : Nếu m ≠ 1
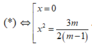
Hàm số có cực đại mà ko có cực tiểu
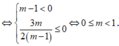
Kết hợp 2 trường hợp : m ∈ [ 0 ; 1 ]
Chọn B.
Hàm số trùng phương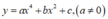
có một cực tiểu mà không có cực đại khi