Cho hàm số (d):y=2x và (d'):y=x+1
a. vẽ đồ thị hai hàm số trên cùng một mặt phẳng toạ độ
b. Tìm toạ độ giao điểm cưa hai đồ thị bằng phép tính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 12 2022
a, Vẽ đồ thị hàm số y = 2x - 4
- Giao đồ thị với trục Ox là điểm có tung độ bằng 0 ; y = 0
=> 2x - 4 = 0 => x = 4/2 => x= 2
Đồ thị cắt trục hành tại A ( 2; 0)
- Giao đồ thị với trục Oy là điểm cs hoành độ bằng 0 ; x = 0
=> y = 0-4 = -4
Đồ thị cắt trục tung tại B ( 0; -4)
Tính khoảng cách từ điểm O đến đt (d) : y = 2x - 4
=> 2x - 4 - y = 0
=> 2x - y - 4 = 0 (d1)
Khoảng cách từ O đến d chính là khoảng cách từ O đến (d1)
Điểm O(0 ;0)
d(0; d1) = \(\dfrac{|2.0-0-4|}{\sqrt{2^2+1^1}}\)
d(O; d1) = \(\dfrac{4}{\sqrt{5}}\) = \(\dfrac{4\sqrt{5}}{5}\)
b, phương trình đt d' có dạng : ax + b
d'//d \(\Leftrightarrow\) a = 2; b # -4
Phương trình đt d' có dạng : 2x + b
Vì d' đi qua A ( 0; 3) nên tọa độ điểm A thỏa mãn pt đường thẳng d.
Thay tọa độ điểm A vào pt đt d' ta có :
2. 0 + b = 3
0 + b = 3
b = 3
vậy các hệ số a; b của đt d' son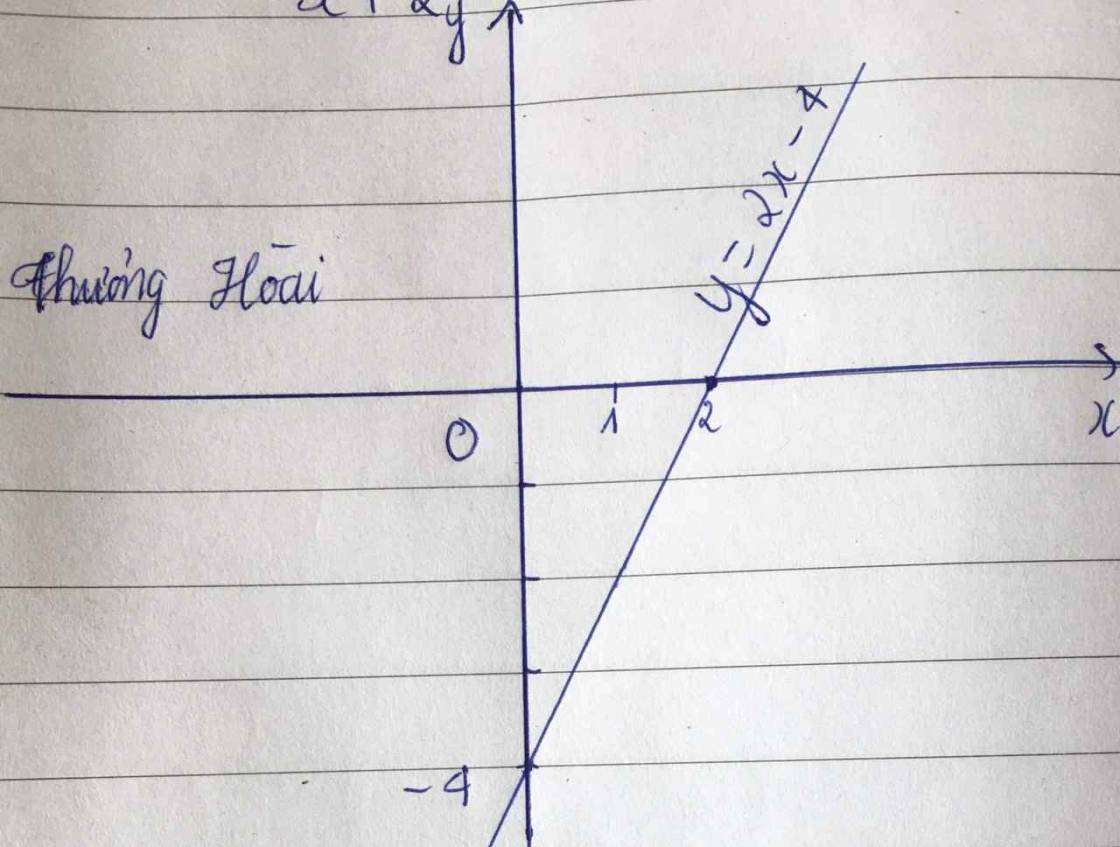
g song với d và đi qua A( 0; 3) lần lượt là : 2; 3
6 tháng 8 2023
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: 
CM
16 tháng 12 2017
Chọn A.
Phương trình hoành độ giao điểm:
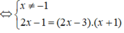
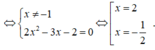
Vậy số giao điểm là 2.
23 tháng 12 2020
Để d song song với d' thì \(\left\{{}\begin{matrix}m^2=2\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm\sqrt{2}\\m\ne1\end{matrix}\right.\Leftrightarrow m\in\left\{\sqrt{2};-\sqrt{2}\right\}\)(1)
Để d' cắt trục hoành thì y=0
Thay y=0 vào hàm số \(y=m^2x+m\), ta được:
\(m^2x+m=0\)
\(\Leftrightarrow x\cdot m^2=-m\)
\(\Leftrightarrow x=\dfrac{-m}{m^2}=\dfrac{-1}{m}\)
Để d' cắt trục hoành tại điểm có hoành độ âm thì \(x< 0\)
\(\Leftrightarrow\dfrac{-1}{m}< 0\)
\(\Leftrightarrow m>0\)(2)
Từ (1) và (2) suy ra \(m=\sqrt{2}\)
Vậy: Để d//d' và d' cắt trục hoành tại điểm có hoành độ âm thì \(m=\sqrt{2}\)
16 tháng 12 2021
\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5 tháng 12 2023
a: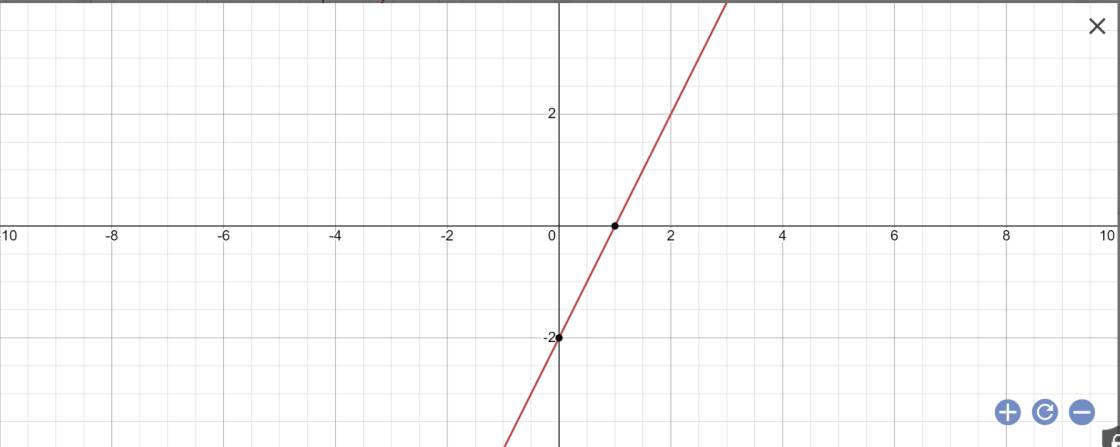 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
N
6 tháng 12 2021
a. \(PTHDGD:\left(d\right)-\left(d'\right):2x+3=x-1\)
\(\Rightarrow x=-4\left(1\right)\)
Thay (1) vào (d'): \(y=-4-1=-5\)
\(\Rightarrow M\left(-4;-5\right)\)
6 tháng 12 2021
\(a,\text{PT hoành độ giao điểm: }2x+3=x-1\\ \Leftrightarrow x=-4\Leftrightarrow y=-5\\ \Leftrightarrow M\left(-4;-5\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}-2a+b=3\\a=2;b\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\)
31 tháng 8 2023
b: Phương trình hoành độ giao điểm là:
2x+1=x+3
=>2x-x=3-1
=>x=2
Thay x=2 vào y=x+3, ta được:
y=2+3=5
a: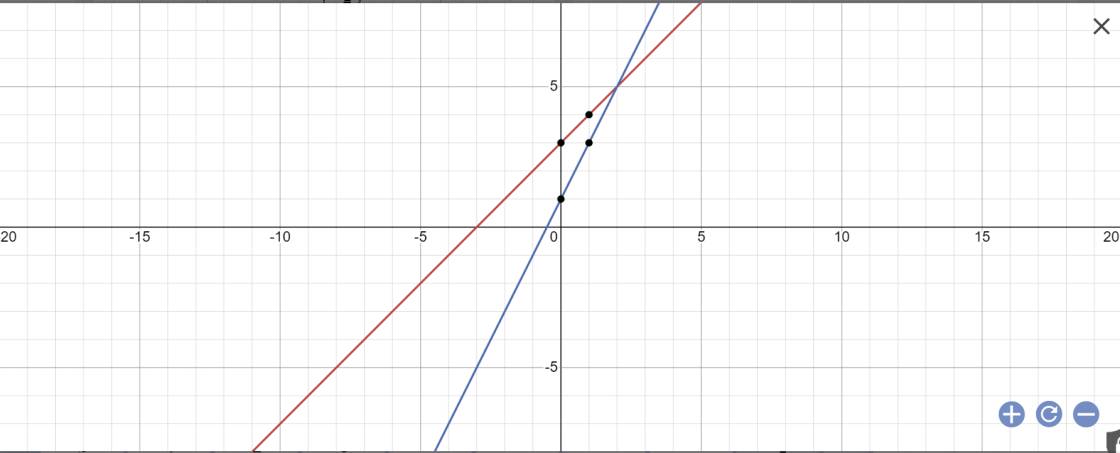 
b. PTHDGD: \(2x=x+1\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)
Vậy tọa độ giao điểm 2 đt là \(A\left(1;2\right)\)
vậy còn phần A với vẽ hình thì làm sao vậy ạ