Điểm A biểu diễn số phức z ≠ 0, điểm B biểu diễn số phức w. Biết w = ( 1 - i ) z 2 . Chọn khẳng định đúng.
A. A O B ^ = 60 0
B. Tam giác OAB vuông cân
C. A B O ^ = 30 0
D. O là trung điểm AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Tọa độ điểm A và Bb lần lượt là: A(3;2) và B(2;3). A B → - 1 ; 1
Đường thẳng y = x hay x - y = 0 có vecto pháp tuyến là n → 1 ; 1
Do 2 vecto n → ; A B → là 2 vecto cùng phương nên đường thẳng AB vuông góc với đường thẳng y = x.
Gọi M(5/2; 5/2) là trung điểm AB; ta thấy M thuộc đường thẳng y = x. Do đó đường thẳng y = x là đường trung trực của AB.
Hay A và B đối xứng nhau qua y = x.

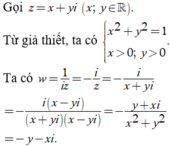
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-y;-x) (đều có hoành độ và tung độ âm). Đồng thời ![]()
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn C.

Đáp án C
Đặt z = x + y i ; w = a + b i , x ; y ; a ; b ∈ ℝ
z − w = z + w ⇔ x + y i − a − b i = x + y i + a + b i
⇔ x − a 2 + y − b 2 = x + a 2 + y + b 2 ⇔ a x + b y = 0
Mặt khác
z w = x + y i a + b i = x + y i a − b i a 2 + b 2 = − a y + b x i a 2 + b 2
Suy ra z w là một số thuần ảo, vậy điểm biểu diễn số phức z w thuộc trục Oy
Đáp án B