Trong thí nghiệm về giao thoa sóng nước, hai nguồn A và B cách nhau 8 cm, dao động điều hòa theo phương vuông góc mặt nước, cùng pha, cùng biên độ, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Ở mặt nước, gọi \(\Delta\) là đường trung trực của đoạn AB. Trên \(\Delta\) điểm M cách AB 3cm; điểm N dao động ngược pha với M và gần M nhất sẽ cách M một đoạn có giá trị...
Đọc tiếp
Trong thí nghiệm về giao thoa sóng nước, hai nguồn A và B cách nhau 8 cm, dao động điều hòa theo phương vuông góc mặt nước, cùng pha, cùng biên độ, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Ở mặt nước, gọi \(\Delta\) là đường trung trực của đoạn AB. Trên \(\Delta\) điểm M cách AB 3cm; điểm N dao động ngược pha với M và gần M nhất sẽ cách M một đoạn có giá trị ?






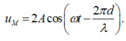
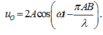
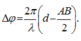
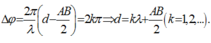
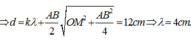
Đáp án B
Pha dao động của các điểm trên A C : φ = π d 1 + d 1 2 + 16 2 λ → để một điểm trên A C vuông pha với nguồn thì φ = π d 1 + d 1 2 + 16 2 λ = 2 k + 1 π 4 → d 1 + d 1 2 + 16 2 = 2 k + 1 λ 4
Với 0 ≤ d 1 ≤ 12 c m → có 3 giá trị