Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có:
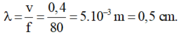
+ Độ lệch pha dao động của 2 điểm M, N trên đường trung trực d của AB là:
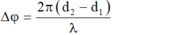
+ N dao động cùng pha với M khi :
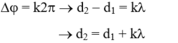
+ Hai điểm M1 và M2 gần M nhất dao động cùng pha với M ứng với:
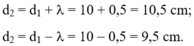
- Ta có:

- Vậy điểm dao động cùng pha gần M nhất ứng với điểm M2 và cách M 8 mm gần 7,8 mm nhất.

+ Ta có: λ = v f = 0 , 4 80 = 5 . 10 - 3 m = 0,5 cm.
+ Độ lệch pha dao động của 2 điểm M, N trên đường trung trực d của AB là: ∆ φ = 2 π ( d 2 - d 1 ) λ
+ N dao động cùng pha với M khi Dj = k2p → d2 - d1 = k λ → d2 = d1 + k λ
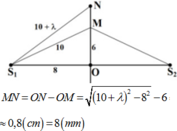
+ Hai điểm M1 và M2 gần M nhất dao động cùng pha với M ứng với: d2 = d1 + λ = 10 + 0,5 = 10,5 cm
Và d2 = d1 - λ = 10 - 0,5 = 9,5 cm.
+ Ta có: MM1 = MH - M1H mà M H = 10 2 - 8 2 = 6 cm và M 1 H = 9 , 5 2 - 8 2 = 5 , 12 cm → MM1 = 0,88 cm = 8,8 mm
MM2 = M2H - MH mà M 2 H = 10 , 5 2 - 8 2 = 6 , 8 cm → MM2 = 0,8 cm = 8 mm.
Vậy điểm dao động cùng pha gần M nhất ứng với điểm M2 và cách M 8 mm → gần 7,8 mm nhất.
Đáp án A

Đáp án A.
Lời giải chi tiết:
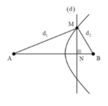
Giả sử hai nguồn có phương trình dao động ![]()
Gọi d là khoảng cách từ M tới 2 nguồn, phương trình sóng tại M là:
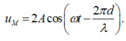
Phương trình sóng tại O là: 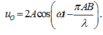
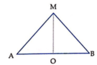
Độ lệch pha giữa chúng 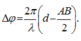
Để M và O cùng pha thì:
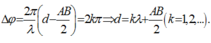
Vì M gần O nhất ứng với k=1
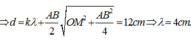
Tốc độ truyền sóng ![]()

Đáp án D
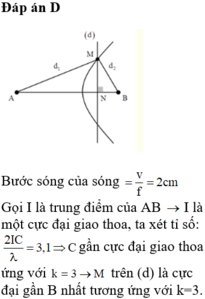
+ Bước sóng của sóng λ = v f = 2 c m
+ Gọi I là trung điểm của → là một cực đại giao thoa, ta xét tỉ số:
2 I C λ = 3 , 1 ⇒ C gần cực đại giao thoa ứng với k=3trên (d) là cực đại gần B nhất tương ứng
với k = 3.
Ta có:
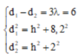
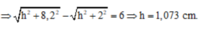

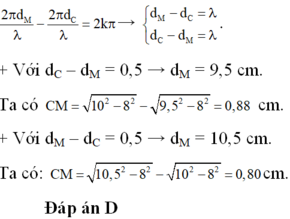


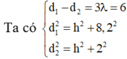
\(\lambda=\dfrac{v}{f}=\dfrac{40}{80}=0,5\left(cm\right)\)
\(\omega=2\pi f=2\pi.80=160\pi\left(rad\right)\)
Ta có:
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
PT sóng tổng hợp tại M:
\(u_M=16cos\left(160\pi t-20\pi\right)\left(cm\right)\)
hay \(u_M=16cos\left(160\pi t\right)\left(cm\right)\)
Pt sóng tổng hợp tại N cách A một khoảng \(d\left(cm\right)\):
\(u_N=16cos\left(160\pi t-4\pi d\right)\left(cm\right)\)
Mà N dao động ngược pha với M nên:
\(4\pi d=\pi+k2\pi\left(k\in Z\right)\)
\(\Leftrightarrow d=\dfrac{1}{4}+\dfrac{k}{2}\left(cm\right)\left(d\ge4\right)\)
Để \(d_{\left(N;M\right)}min\) thì \(\left|3-\sqrt{d^2-4^2}\right|min\)\(\Rightarrow d=\dfrac{1}{4}+\dfrac{10}{2}=\dfrac{21}{4}\left(cm\right)\)
Khi đó \(d_{\left(N;M\right)}=\dfrac{-12+\sqrt{185}}{4}\approx0,4\left(cm\right)\)
Cách khác:
Dùng độ lệch pha dao động của hai điểm M và N.
Ta có: \(\lambda=\dfrac{v}{f}=\dfrac{40}{80}=0,5cm\)
Độ lệch pha dao động của hai điểm M và N trên trung trực của MN: \(\Delta\varphi=\dfrac{2\pi\left(d_2-d_1\right)}{\lambda}\)
M dao động cùng pha với N nên \(d_2-d_1=k\lambda\)
\(\Rightarrow d_2=3+0,5=3,5cm\)
\(MM_1=MH-M_1H=\left(8-3\right)-\sqrt{4^2-\left(3-0,5\right)^2}=1,88cm\)
\(MM_2=MH-M_2H=5-\sqrt{4^2-3,5^2}=3,06cm\)