Bài 1 : Cho x , y là các số nguyên . Chứng tỏ rằng 5x + 7y là bội của 17 khi và chỉ khi x + 6y là bội của 17 ( Trình bày rõ => like )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5x + 47y (1)
= 5x + 30y + 17y = 5(x+6y) + 17y.
17y luôn chia hết cho 17. Vậy để (1) chia hết cho 17 <=> x + 6y chia hết 17

Nguyễn Linh Chi Vâng ạ, vậy e thử làm cách này, sẽ giải quyết được cả hai chiều, mong cô xem hộ em ạ :
Đặt \(A=6x+11y\), \(B=x+7y\)
Ta có : \(5A+B=5\left(6x+11y\right)+\left(x+7y\right)=31x+62y\)
Rõ ràng thấy, \(5A+B⋮13\forall x,y\inℤ\). Do đó :
+) Nếu \(A⋮31\)thì \(5A⋮31\) \(\Rightarrow B⋮31\)
+) Nếu \(B⋮31\) thì \(5A⋮31\) mà \(\left(5,31\right)=1\) nên \(A⋮31\)
Vậy : bài toán được chứng minh !!

Vì \(x+6y\)là bội của 17
\(\Rightarrow5\left(x+6y\right)=5x+30y\)cũng là bội của 17
mà \(17y⋮17\)\(\Rightarrow17y\)là bội của 17
\(\Rightarrow5x+30y+17y=5x+47y\)là bội của 17 ( đpcm )

Với x+6y chia hết cho 17
Ta có
\(3\left(5x+47y\right)+2\left(x+6y\right)\)
\(=15x+141y+2x+12y\)
\(=17x+153y\) chia hết cho 17
Mặt khác 2(x+6y) chia hết cho 17
=> 3(5x+47y) chia hết cho 17
Mà (3;47)=1
=> 5x+47y chia hết cho 17
=> đpcm
Câu hỏi của Công Chúa Tình Yêu - Toán lớp 6 | Học trực tuyến

5x + 47y = x + 6y + 4x + 24y + 17y = ( x + 6y ) + 4( x + 6y) + 17y = ( x + 6y ) ( 1 + 4 ) + 17y = 5 ( x + 6y ) + 17y
Vì 17y luôn chia hết cho 17 nên 5 ( x+ 6y ) + 17y \(⋮\)17 \(\Leftrightarrow\)x + 6y \(⋮\)17
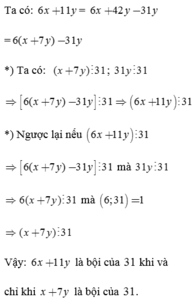
Ta có: x + 6y chia hết cho 17 => 5(x + 6y) chia hết cho 17
=> 5x + 30y chia hết cho 17
Lại có : 5x + 30y chia hét cho 17
17y chia hết cho 17
=> 5x + 30y + 17 chia hết cho 17
5x + 47y chia hết cho 17
Vậy 5x + 47y chia hết cho 17
Đúng thì tick nha! Hà My Trần
ta có 5x+7y chia hết cho 17 <=> x+6y chia hết cho 17
ta đặt M= 4(x+6y)-(5x+7y)
=>M=17y chia hết cho 17
Mà 5x+7y chia hết cho 17 ; M cũng chia hết cho 17
=> x+6y chia hết cho 17 vì (17;4)=1
vậy 5x+7y chia hết cho 17<=> x+6y chia hết cho 17
lưu ý: chia hết và bộ cũng giống nhau