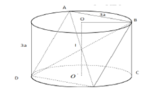
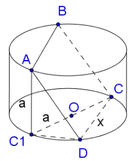
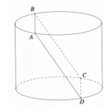
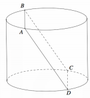
Cho một hình trụ (T) có chiều cao và bán kính đều bằng 3a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ (T). Tính cạnh của hình vuông này.
A. 3 a 5
B. 6 a
C. 3 a 10 2
D. 3 a

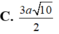



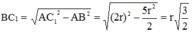
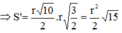
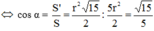
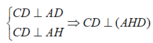

Đáp án C
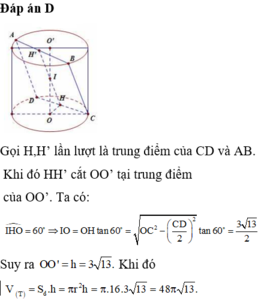
Phương pháp: Gọi là tâm hình vuông ⇒ I ∈ O O ' .
Sử dụng định lý Py-ta-go trong tam giác vuông để tính AB.
Cách giải:
Ta có: I B = O I 2 + O B 2 = 9 a 2 4 + 9 a 2 = 3 a 5 2
⇒ A B = B I . 2 = 3 a 10 2