Cho hình chóp S.ABCD có các cạnh bên bằng a, góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng a (a thay đổi). Tìm giá trị lớn nhất của thể tích của S.ABCD


![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
H là tâm đường tròn nội tiếp đáy.
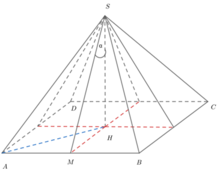
Cách giải: Vì góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α nên H là tâm đường tròn nội tiếp ABCD.
Vì các cạnh bên hình chóp S.ABCD bằng a nên H là tâm đường tròn ngoại tiếp ABCD.
Vậy ABCD là hình vuông. Suy ra S.ABCD là hình chóp tứ giác đều.

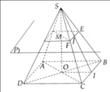
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
Chọn D