Bài 1: Cho (d1): y = 3x + 2 (d2): y = x – 2 a) Tìm tọa độ giao điểm của (d1) và (d2) với trục hoành b) Tìm tọa độ giao điểm của (d1) và (d2) với trục tung c) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy d) Tìm tọa độ giao điểm của (d1) và (d2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 12 2021
\(m=1\Leftrightarrow\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=2x-2\end{matrix}\right.\\ \text{PTHDGD: }-2x-2=2x-2\Leftrightarrow x=0\Leftrightarrow y=-2\Leftrightarrow A\left(0;-2\right)\\ \text{PT giao Ox: }\left\{{}\begin{matrix}y=0\Leftrightarrow x=-1\Leftrightarrow B\left(-1;0\right)\Leftrightarrow OB=1\\y=0\Leftrightarrow x=1\Leftrightarrow C\left(1;0\right)\Leftrightarrow OC=1\end{matrix}\right.\\ \Leftrightarrow BC=1+1=2\\ AB=AC=\sqrt{2^2+1^2}=\sqrt{3}\\ OA=\left|-2\right|=2\\ \Leftrightarrow P_{ABC}=AB+BC+CA=2+2\sqrt{3}\left(đvd\right)\\ S_{ABC}=\dfrac{1}{2}OA\cdot BC=\dfrac{1}{2}\cdot2\cdot2=2\left(đvdt\right)\)
Gọi góc đó là \(\alpha\)
Vì \(2>0\Leftrightarrow\alpha< 90^0\)
\(\tan\alpha=2\Leftrightarrow\alpha\approx63^0\)
13 tháng 11 2023
a: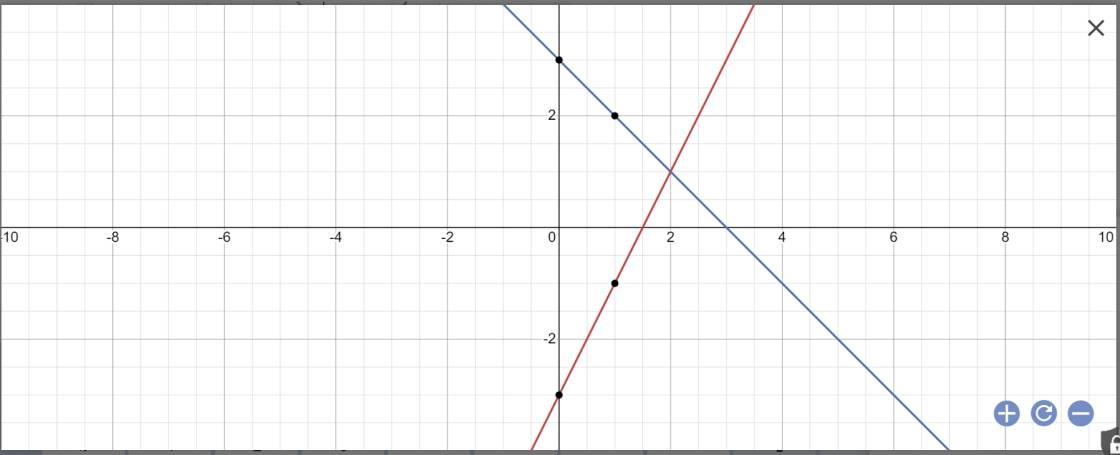 
b: Phương trình hoành độ giao điểm là:
2x-3=3-x
=>3x=6
=>x=6/3=2
Thay x=2 vào y=3-x, ta được:
\(y=3-2=1\)
6 tháng 8 2021
a, bạn tự vẽ nhé
b, Hoành độ giao điểm thỏa mãn phương trình
\(2x-3=-3x+7\Leftrightarrow5x=10\Leftrightarrow x=2\)
Thay vào ptđt d1 ta được : \(y=4-3=1\)
Vậy d1 cắt d2 tại A(2;1)
16 tháng 11 2023
a: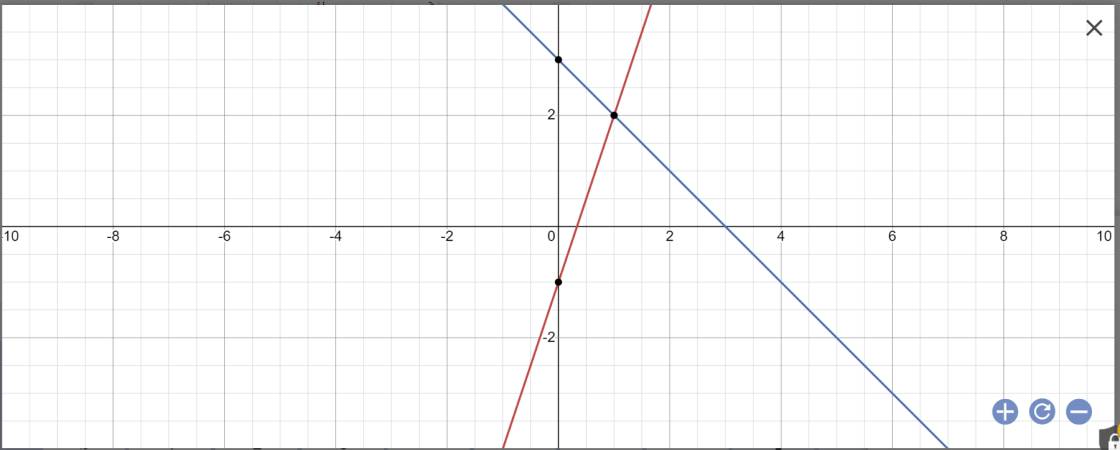 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 11 2023
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C
6 tháng 7 2016
(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU
\(b,\) PT hoành độ giao điểm: \(3x+2=x-2\Leftrightarrow x=-2\Leftrightarrow y=-4\Leftrightarrow A\left(-2;-4\right)\)
Vậy \(A\left(-2;-4\right)\) là tọa độ giao điểm