Cho hàm số f x = log 2 x log 2 x + 1 . Tính tổng S = f 2 − 100 + f 2 − 99 + ... + f 2 − 2 + f 2 0 + f 2 1 + ... + f 2 98
A. S=99
B.S=100
C.S=200
D. S=198
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=\dfrac{1}{x\cdot ln10}\)
=>\(f'\left(\dfrac{1}{2}\right)=\dfrac{1}{\dfrac{1}{2}\cdot ln10}=\dfrac{2}{ln10}\)

Đáp án D
Ý tưởng bài toán: Với bài toán dạng này, ta thường chọn hai giá trị a, b bất kì, tính tổng f ( a ) + f ( b ) và tìm mối quan hệ giữa hai giá trị a, b.
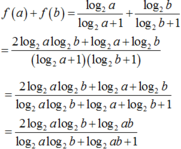
Cần chọn hai giá trị a, b sao cho tử rút gọn được với mẫu.
Ta thường chọn a + b = k hoặc a b = k . Ở bài toán này ta chọn a b = k .
Nếu a b = 1 4 thì log 2 a b = log 2 1 4 = - 2 .
Suy ra

Vậy với các giá trị a, b thỏa mãn a b = 1 4 thì f ( a ) + f ( b ) = 2 .
Ta có
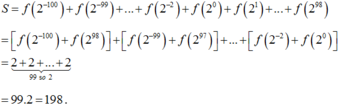

\(a,\left(0,3\right)^{x-3}=1\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\\ b,5^{3x-2}=25\\ \Leftrightarrow3x-2=2\\ \Leftrightarrow3x=4\\ \Leftrightarrow x=\dfrac{4}{3}\\ c,9^{x-2}=243^{x+1}\\ \Leftrightarrow3^{2x-4}=3^{5x+5}\\ \Leftrightarrow2x-4=5x+5\\ \Leftrightarrow3x=-9\\ \Leftrightarrow x=-3\)
d, Điều kiện: \(x>-1;x\ne0\)
\(log_{\dfrac{1}{x}}\left(x+1\right)=-3\\ \Leftrightarrow x+1=x^3\\ x\simeq1,325\left(tm\right)\)
e, Điều kiện: \(x>\dfrac{5}{3}\)
\(log_5\left(3x-5\right)=log_5\left(2x+1\right)\\ \Leftrightarrow3x-5=2x+1\\ \Leftrightarrow x=6\left(tm\right)\)
f, Điều kiện: \(x>\dfrac{1}{2}\)
\(log_{\dfrac{1}{7}}\left(x+9\right)=log_{\dfrac{1}{7}}\left(2x-1\right)\\ \Leftrightarrow x+9=2x-1\\ \Leftrightarrow x=10\left(tm\right)\)

Chọn A
Điều kiện:

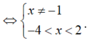
Vậy tập xác định của hàm số f(x) là ![]() suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1
suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
Đáp án D
Ý tưởng bài toán: Với bài toán dạng này, ta thường chọn hai giá trị a, b bất kì, tính tổng f a + f b và tìm mối quan hệ giữa hai giá trị a, b.
f a + f b = log 2 a log 2 a + 1 + log 2 b log 2 b + 1 = 2 log 2 a log 2 b + log 2 a + log 2 b log 2 a + 1 log 2 b + 1
= 2 log 2 a log 2 b + log 2 a + log 2 b log 2 a log 2 b + log 2 a + log 2 b + 1 = 2 log 2 a log 2 b + log 2 a b log 2 a log 2 b + log 2 a b + 1
Cần chọn hai giá trị a, b sao cho tử rút gọn được với mẫu.
Ta thường chọn a+b=k hoặc ab=k. Ở bài toán này ta chọn ab=k.
Nếu a b = 1 4 thì log 2 a b = log 2 1 4 = − 2 .
Suy ra
f a + f b = 2 log 2 a log 2 b − 2 log 2 a log 2 b − 2 + 1 = 2
Vậy với các giá trị a, b thỏa mãn a b = 1 4 thì f a + f b = 2 .
Ta có
S = f 2 − 100 + f 2 − 99 + ... + f 2 − 2 + f 2 0 + f 2 1 + ... + f 2 98
= f 2 − 100 + f 2 98 + f 2 − 99 + f 2 97 + ... + f 2 − 2 + f 2 0 = 2 + 2 + ... + 2 ⏟ 99 s o 2
= 99.2 = 198 .