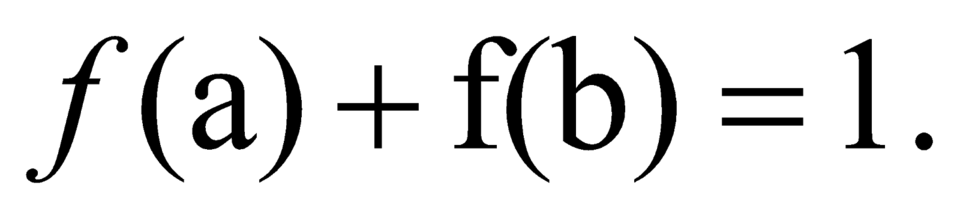Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
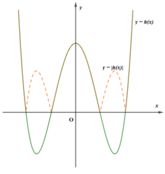
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
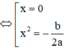
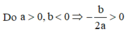
![]()
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7

Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A

Chọn C.
Đặt t = f ( x ) → d t = f ' x d x . Đổi cận: x = 2016 → t = f ( 2016 ) = a x = 2017 → t = f ( 2017 ) = b
Khi đó
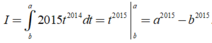

Đáp án D
Ý tưởng bài toán: Với bài toán dạng này, ta thường chọn hai giá trị a, b bất kì, tính tổng f ( a ) + f ( b ) và tìm mối quan hệ giữa hai giá trị a, b.
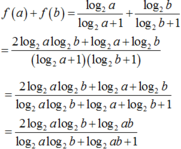
Cần chọn hai giá trị a, b sao cho tử rút gọn được với mẫu.
Ta thường chọn a + b = k hoặc a b = k . Ở bài toán này ta chọn a b = k .
Nếu a b = 1 4 thì log 2 a b = log 2 1 4 = - 2 .
Suy ra

Vậy với các giá trị a, b thỏa mãn a b = 1 4 thì f ( a ) + f ( b ) = 2 .
Ta có
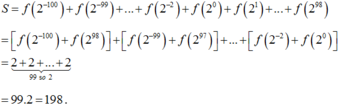
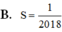
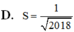

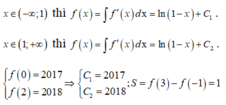
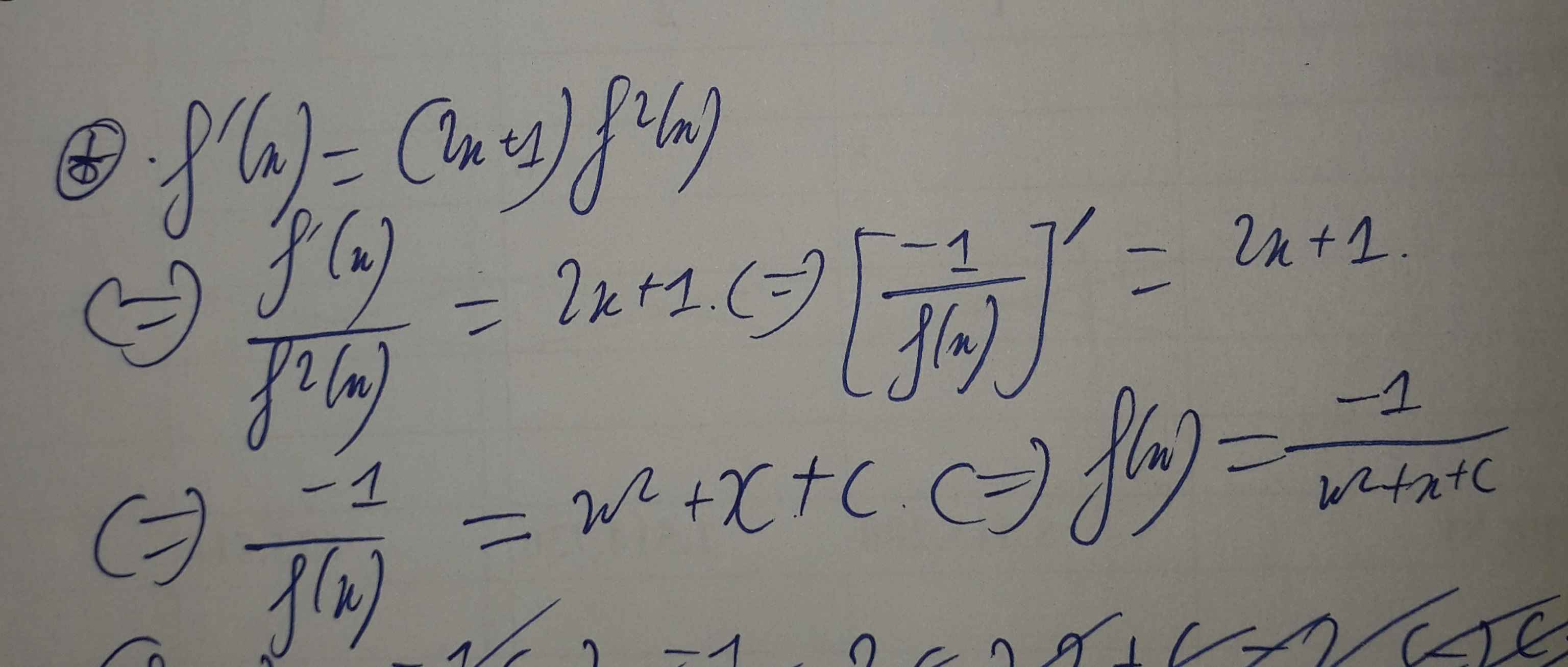
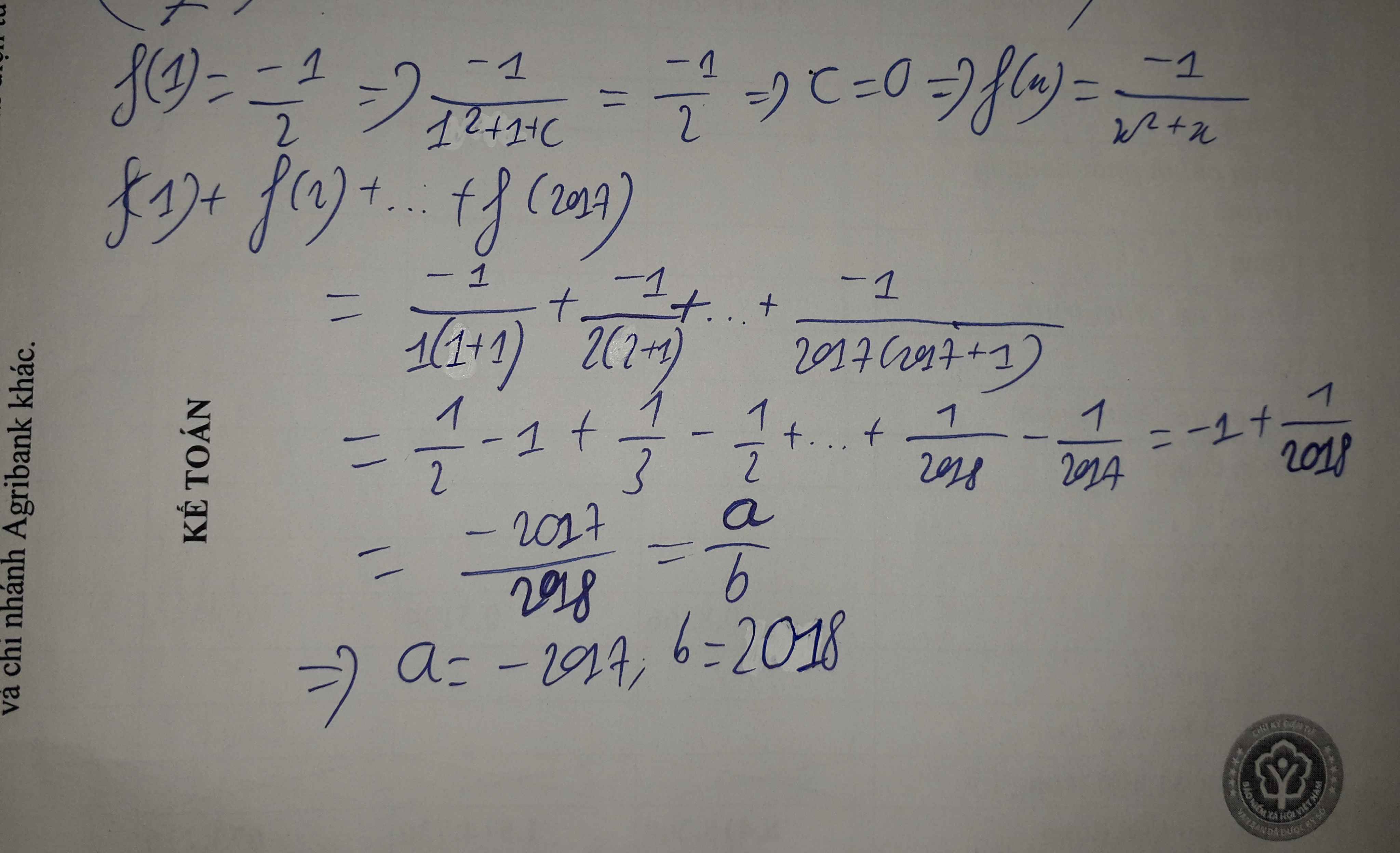
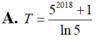
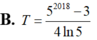
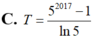
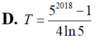

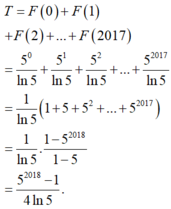
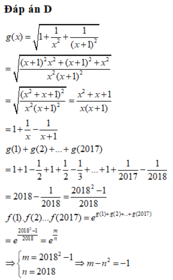
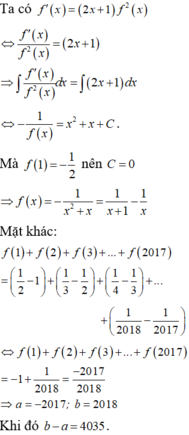
Đáp án C
Chứng minh nhận xét: Nếu a + b = 1 thì