Cho hai số thực a và b thỏa mãn: log a + b + 1 2 a 2 + 9 b 2 + 1 + log 6 a b + 1 a + b + 1 2 6 a b + 1 3 = 0 Khi đó giá trị của biểu thức P = 2a + 3b bằng
A. 2
B. 4
C. 5
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

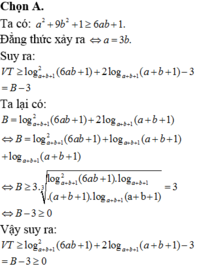
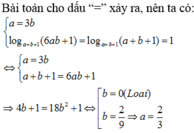


\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)

Chọn A.
Dễ thấy un là cấp số nhân với q = 10
Ta có: u8 = 107u1; u10 = 109u1
Do đó PT ![]()
![]()
![]()
Giải PT ta được logu1 = -17 ⇔ u1 = 10-17 ⇒ u2018 = 102017 u1 = 102000