Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(log_65=\dfrac{1}{log_56}=\dfrac{1}{log_52+log_53}=\dfrac{1}{a+b}\)
=>Chọn B

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)

a, Hàm số \(y=log_{\dfrac{1}{2}}x\) có cơ số \(\dfrac{1}{2}< 1\) nên hàm số nghịch biến trên \(\left(0;+\infty\right)\)
Mà \(4,8< 5,2\Rightarrow log_{\dfrac{1}{2}}4,8>log_{\dfrac{1}{2}}5,2\)
b, Ta có: \(log_{\sqrt{5}}2=2log_52=log_54\)
Hàm số \(y=log_5x\) có cơ số 5 > 1 nên hàm số đồng biến trên \(\left(0;+\infty\right)\)
Do \(4>2\sqrt{2}\Rightarrow log_54>log_52\sqrt{2}\Rightarrow log_{\sqrt{5}}2>log_52\sqrt{2}\)
c, Ta có: \(-log_{\dfrac{1}{4}}2=-\dfrac{1}{2}log_{\dfrac{1}{2}}2=log_{\dfrac{1}{2}}\dfrac{1}{\sqrt{2}}\)
Hàm số \(y=log_{\dfrac{1}{2}}x\) có cơ số \(\dfrac{1}{2}< 1\) nên nghịch biến trên \(\left(0;+\infty\right)\)
Do \(\dfrac{1}{\sqrt{2}}>0,4\Rightarrow log_{\dfrac{1}{2}}\dfrac{1}{\sqrt{2}}< log_{\dfrac{1}{2}}0,4\Rightarrow-log_{\dfrac{1}{4}}2< log_{\dfrac{1}{2}}0,4\)

\({a^{\frac{1}{2}}} = b \Leftrightarrow {\log _a}b = \frac{1}{2} \Leftrightarrow 2{\log _a}b = 1\)
Chọn B.

\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)
\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)
c, ĐK: \(x-2>0\Rightarrow x>2\)
\(2log_5\left(x-2\right)=log_59\\
\Leftrightarrow log_5\left(x-2\right)^2=log_59\\
\Leftrightarrow\left(x-2\right)^2=3^2\\
\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.
d, ĐK: \(x-1>0\Leftrightarrow x>1\)
\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)

\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

a: \(log_22^{-13}=-13\)
b: \(lne^{\sqrt{2}}=\sqrt{2}\)
c: \(log_816-log_82=log_8\left(\dfrac{16}{2}\right)=log_88=1\)
c: \(log_26\cdot log_68=log_28=3\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
Chọn A.
Dễ thấy un là cấp số nhân với q = 10
Ta có: u8 = 107u1; u10 = 109u1
Do đó PT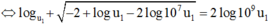
Giải PT ta được logu1 = -17 ⇔ u1 = 10-17 ⇒ u2018 = 102017 u1 = 102000