Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,a^{log_ab^{\alpha}}=c\Leftrightarrow log_ac=log_ab^{\alpha}\Leftrightarrow c=b^{\alpha}\Rightarrow a^{log_ab^{\alpha}}=b^{\alpha}\\ a^{\alpha log_ab}=c\Leftrightarrow\alpha log_ab=log_ac\Leftrightarrow log_ab^{\alpha}=log_ac\Leftrightarrow b^{\alpha}=c\Rightarrow a^{\alpha log_ab}=b^{\alpha}\\ \Rightarrow a^{log_ab^{\alpha}}=a^{\alpha log_ab}\)
\(b,a^{log_ab^{\alpha}}=a^{\alpha log_ab}\\ \Rightarrow log_ab^{\alpha}=\alpha log_ab\)

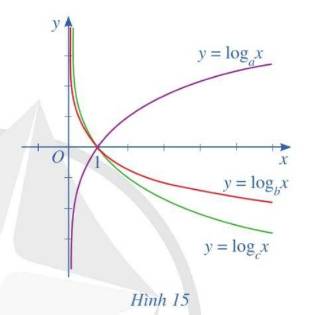
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

\(a,log_a1=c\Leftrightarrow a^c=1\Leftrightarrow c=0\Rightarrow log_a1=0\\ b,log_aa=c\Leftrightarrow a^c=a\Leftrightarrow c=1\Rightarrow log_aa=1\\ c,log_aa^c=b\Leftrightarrow a^b=a^c\Leftrightarrow b=c\Rightarrow log_aa^c=c\\ d,a^{log_ab}=c\Leftrightarrow log_ab=log_ac\Leftrightarrow b=c\Rightarrow a^{log_ab}=b\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

\({a^{\frac{1}{2}}} = b \Leftrightarrow {\log _a}b = \frac{1}{2} \Leftrightarrow 2{\log _a}b = 1\)
Chọn B.

a) \(\log_a\left(a^2b\right)=\log_aa^2+\log_ab=2.\log_aa+\log_ab=2.1+2=4\)
b) \(\log_a\dfrac{a\sqrt{a}}{b\sqrt[3]{a}}=\log_a\left(a\sqrt{a}\right)-\log_a\left(b\sqrt[3]{b}\right)=\log_aa^{\dfrac{3}{2}}-\log_ab^{\dfrac{4}{3}}=\dfrac{3}{2}.\log_aa-\dfrac{4}{3}\log_ab=\dfrac{3}{2}.1-\dfrac{4}{3}.2=-\dfrac{7}{6}\)
c) \(\log_a\left(2b\right)+\log_a\left(\dfrac{b^2}{2}\right)=\log_a2+\log_ab+\log_ab^2-\log_a2=\log_ab+2\log_ab=3\log_ab=3.2=6\)
a: \(=log_aa^2+log_ab=2+2=4\)
b: \(log_a\left(\dfrac{a\sqrt{a}}{b\sqrt[3]{b}}\right)=log_aa^{\dfrac{3}{2}}-log_ab^{\dfrac{4}{3}}\)
=3/2-4/3*2
=3/2-8/3
=9/6-16/6=-7/6
c: \(log_a\left(2b\right)+log_a\left(\dfrac{b^2}{2}\right)\)
\(=log_a\left(2b\cdot\dfrac{b^2}{2}\right)=log_a\left(b^3\right)=3\cdot2=6\)

a,Ta có: \(a^6=\left(a^{\dfrac{3}{5}}\right)^{10}=b^{10}\\ a^3b=\left(a^{\dfrac{3}{5}}\right)^5\cdot b=b^5\cdot b=b^6\\ \dfrac{a^9}{b^9}=\dfrac{\left(a^{\dfrac{3}{5}}\right)^{15}}{b^9}=\dfrac{b^{15}}{b^9}=b^6\)
b, \(log_ab=log_aa^{\dfrac{3}{5}}=\dfrac{3}{5}\\ log_a\left(a^2b^5\right)=log_a\left(a^2\cdot a^3\right)=log_a\left(a^5\right)=5\\ log_{\sqrt[5]{a}}\left(\dfrac{a}{b}\right)=5log_a\left(\dfrac{a}{a^{\dfrac{3}{5}}}\right)=5log_a\left(a^{\dfrac{2}{5}}\right)=2\)
a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)