Số tiếp tuyến với đồ thị hàm số y= x3 – 3x2-2 sao cho tiếp tuyến song song với đường thẳng y=9x - 29 là:
A. 0
B. 2
C. 3
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


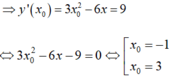
![]()
![]()
![]()
![]()

Chọn D.
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số

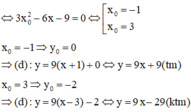

Gọi ![]() là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
Theo giả thiết, ta có 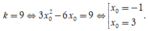
Với 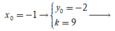 Phương trình tiếp tuyến cần tìm là: y = 9x + 7 (loại)(vì trùng với đường thẳng đã cho).
Phương trình tiếp tuyến cần tìm là: y = 9x + 7 (loại)(vì trùng với đường thẳng đã cho).
Với 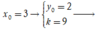 Phương trình tiếp tuyến cần tìm là: y = 9x - 25
Phương trình tiếp tuyến cần tìm là: y = 9x - 25
Chọn B.

Chọn D.
Ta có: y’ = -3x2 + 6x. Lấy điểm M(xo; yo) ∈ (C).
Tiếp tuyến tại Msong song với đường thẳng y = -9x suy ra y’(xo) = -9
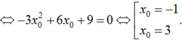
Với xo = -1 ⇒ yo = 2 ta có phương trình tiếp tuyến: y = -9x - 7
Với xo = 3 ⇒ yo = -2 ta có phương trình tiếp tuyến: y = -9x + 25
Vậy có 2 tiếp tuyến thỏa mãn.

Gọi x 0 , y 0 là tọa độ tiếp điểm của đồ thị (C ) và tiếp tuyến ∆.
- Đường thẳng d :
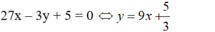
- Vì tiếp tuyến ∆ // d nên tiếp tuyến ∆ có hệ số góc k= 9.
- Theo 4) có hai tiếp tuyến có hệ số góc k = 9 là:
y = 9x – 4 và y = 9x + 28.

Đáp án B
Ta có: y ' = 3 x 2 + 6 x − 2
Tiếp tuyến song song với đường thẳng:
x + y − 3 = 0 y = 2 x + 3 ⇒ y ' = − 2 ⇔ x = 0 x = 2
Với x = 0 ⇒ y = − 1
⇒ P T T T : y = − 2 x − 1 h a y 2 x + y + 1 = 0
Với x = 2 ⇒ y = 15
⇒ P T T T : y = − 2 x − 2 + 15 h a y 2 x + y − 19 = 0

Đáp án B
Ta có: y ' = 3 x 2 + 6 x − 2
Tiếp tuyến song song với đường thẳng
x + y − 3 = 0 y = − 2 x + 3 ⇒ y ' = − 2 ⇔ x = 0 x = 2
Với x = 0 ⇒ y = − 1 ⇒ P T T T : y = − 2 x − 1 h a y 2 x + y + 1 = 0
Với x = 2 ⇒ y = 15 ⇒ P T T T : y = − 2 x − 2 + 15 h a y 2 x + y − 19 = 0

- Tập xác định: D = R
- Đạo hàm: y ’ = 3 x 2 – 6 x
- Do tiếp tuyến Δ song song với đường thẳng (d): y = 9x + 10 nên hệ số góc của tiếp tuyến là:
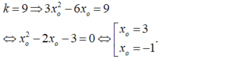
- Ứng với 2 giá trị x 0 ta viết được hai phương trình tiếp tuyến thỏa mãn bài.
Chọn C.