Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tập xác định: D = R.
- Đạo hàm: y ' = 3 x 2 - 6 x .
- Đường thẳng d: y = 9x + 100 có hệ số góc k = 9.
- Vì tiếp tuyến song song với đường thẳng d nên k t t = 9 .
- Ta có:
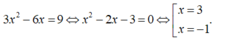
- Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán.
Chọn C

Chọn D.
Ta có: y’ = -3x2 + 6x. Lấy điểm M(xo; yo) ∈ (C).
Tiếp tuyến tại Msong song với đường thẳng y = -9x suy ra y’(xo) = -9
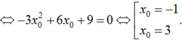
Với xo = -1 ⇒ yo = 2 ta có phương trình tiếp tuyến: y = -9x - 7
Với xo = 3 ⇒ yo = -2 ta có phương trình tiếp tuyến: y = -9x + 25
Vậy có 2 tiếp tuyến thỏa mãn.

Lời giải:
Để PTTT tại $x=x_0$ song song với trục hoành thì $f'(x_0)=0$ và $f(x_0)\neq 0$
$f'(x)=4x^3-4x=0\Leftrightarrow x=0;1;-1$
Thử các giá trị $x$ này vô $f(x_0)$ xem có khác $0$ hay không ta thu được $x=\pm 1$
Tức là có 2 tiếp tuyến của $(C)$ song song với trục hoành.

\(\left(m^2-3m-5\right)x-y-2m+19=0\)
\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)
Ta có:
\(f'\left(x\right)=-3x^2+4x-1\)
\(f'\left(2\right)=-5\)
Phương trình tiếp tuyến tại A:
\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)
Để hai đường thẳng song song:
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)
\(\Leftrightarrow m=0\)

Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)

Gọi x 0 , y 0 là tọa độ tiếp điểm của đồ thị (C ) và tiếp tuyến ∆.
- Đường thẳng d :
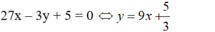
- Vì tiếp tuyến ∆ // d nên tiếp tuyến ∆ có hệ số góc k= 9.
- Theo 4) có hai tiếp tuyến có hệ số góc k = 9 là:
y = 9x – 4 và y = 9x + 28.

a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3
- Tập xác định: D = R
- Đạo hàm: y ’ = 3 x 2 – 6 x
- Do tiếp tuyến Δ song song với đường thẳng (d): y = 9x + 10 nên hệ số góc của tiếp tuyến là:
- Ứng với 2 giá trị x 0 ta viết được hai phương trình tiếp tuyến thỏa mãn bài.
Chọn C.