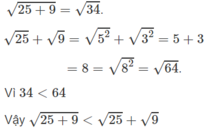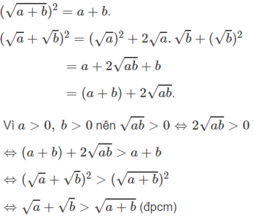So sánh: a) (-25).(-26) với 0;b) (-34).(-72) với -120; c) (-12).(-26) với - 433; d) (-17).5 với (-13).(-3).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
16 tháng 4 2021
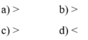
a) Ta có:
+)√25+9=√34+)25+9=34.
+)√25+√9=√52+√32=5+3+)25+9=52+32=5+3
=8=√82=√64=8=82=64.
Vì 34<6434<64 nên √34<√6434<64
Vậy √25+9<√25+√925+9<25+9
b) Với a>0,b>0a>0,b>0, ta có
+)(√a+b)2=a+b+)(a+b)2=a+b.
+)(√a+√b)2=(√a)2+2√a.√b+(√b)2+)(a+b)2=(a)2+2a.b+(b)2
=a+2√ab+b=a+2ab+b
=(a+b)+2√ab=(a+b)+2ab.
Vì a>0, b>0a>0, b>0 nên √ab>0⇔2√ab>0ab>0⇔2ab>0
⇔(a+b)+2√ab>a+b⇔(a+b)+2ab>a+b
⇔(√a+√b)2>(√a+b)2⇔(a+b)2>(a+b)2
⇔√a+√b>√a+b⇔a+b>a+b (đpcm)
17 tháng 4 2021
a, Ta có : \(\sqrt{25+9}=\sqrt{34}\)
\(\sqrt{25}+\sqrt{9}=5+3=8=\sqrt{64}\)
mà 34 < 64 hay \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)
b, \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)
bình phương 2 vế ta được : \(a+b< a+2\sqrt{ab}+b\)
\(\Leftrightarrow2\sqrt{ab}>0\)vì \(a;b>0\)nên đẳng thức này luôn đúng )
Vậy ta có đpcm
VP
1
24 tháng 8 2020
\(A=\frac{24}{26}\div\frac{25}{25}.\)
\(\frac{25}{25}=1.\)
\(A=\frac{24}{26}\div1\)
\(A=\frac{24}{26}.\)
10 tháng 1 2019
2
a,237.(-26)+26.137
=(-237).26+26.137
=26.(-237+137)
=26.(-100)=-2600
b,63.(-25)+25.(-23)
=(-63).25+25.(-23)
=25.{-63+(-23)}
=25.-86=-2150
3,
a,A=(-2)...(-2014)với 0
Xét -2;-3;...;-2014 có 2014-2+1=2013(chữ số)
Vì số chữ số âm lẻ nên tích của chúng là số âm(vì 2013 là số lẻ)
A<0
b,B=(-1)...(-2014) với 0
Xét -1;...;-2014 có 2014-1+1=2014(chữ số)
Vì số chữ số âm chẵn nên tích của chúng là số dương(vì 2014 là số chẵn)
B>0
k cho mình nhé
CM
17 tháng 4 2017
a) ( − 225 ) . ( − 336 ) > 0
b) ( − 112 ) .2. ( − 26 ) . ( − 321 ) < 0
TT
1
17 tháng 4 2018
\(A=10^{25}+\frac{1}{10^{26}}+1=1\cdot10^{25}\)
\(B=10^{26}+\frac{1}{10^{27}}+1=1\cdot10^{26}\)
\(1\cdot10^{25}< 1\cdot10^{26}\Rightarrow A< B\)
OK
25 tháng 9 2017
A = 262 - 242
B = 272 - 252
A = 676 - 576
A = 100
B = 729 - 625
B = 104
=> B > A
25 tháng 9 2017
Em áp dụng hằng đẳng thức A^2 - B^2 = (A - B).(A + B)
A= 26^2 - 24^2 = (26 - 24).(26 + 24) = 2.50 ( = 100)
B= 27^2 - 25^2=(27 - 25).(27 + 25) = 2.51 ( = 101)
( nhẩm ra liền, mà ko cần nhẩm cũng đc ) cùng là tích của 2 nhân với 1 số, mà ta thấy 50 < 51
=> A < B