Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ R: 3x = x2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 9 2019
C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.

CM
19 tháng 1 2019
B: “∃ x ∈ Q : x2 = 2”.
B− : “∀ x ∈ Q : x2 ≠ 2”
B− đúng.
Lưu ý: √2 là số vô tỷ.
PT
1
PT
1

AH
Akai Haruma
Giáo viên
8 tháng 9 2021
Lời giải:
a. Mệnh đề sai, vì $x^2\geq 0>-1$ với mọi $x\in\mathbb{R}$ theo tính chất bình phương 1 sosos.
Mệnh đề phủ định: $\forall x\in\mathbb{R}, x^2\neq -1$
b. Mệnh đề đúng, vì $x^2+x+2=(x+0,5)^2+1,75>0$ với mọi $x\in\mathbb{R}$ nên $x^2+x+2\neq 0$ với mọi $x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}| x^2+x+2=0$
PT
1

CM
19 tháng 11 2019
A: “∀ n ∈ N: n chia hết cho n”
A− : “∃ n ∈ N: n không chia hết cho n”.
A− đúng vì với n = 0 thì n không chia hết cho n.
PT
1

CM
18 tháng 10 2017
Có ít nhất một hình vuông không phải là hình thoi. Mệnh đề sai.
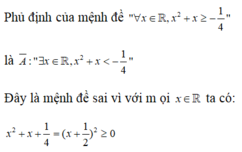
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với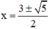
D− thỏa mãn: