Cho các số thực x, y, z thỏa mãn điều kiện x - y + z = 3 x 2 + y 2 + z 2 = 5 . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P = x + y - 2 z + 2 . Tính M + m
A. M + m = 2
B. M + m = 4 3 3
C. M + m = 4
D. M + m = 4 3 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
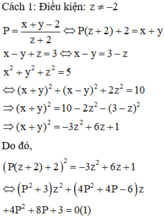

Do đó, P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Trong biểu thức P vai trò của z khác x, y do đó, ta tìm cách rút x, y theo z từ điều kiện ban đầu. Từ đó quy về phương trình ẩn z và tìm điều kiện để phương trình có nghiệm |

Phương trình (2), (3) là các phương trình mặt phẳng
Hai mặt phẳng này cắt nhau theo giao tuyến d có vecto chỉ phương là

Phương trình (4) là phương trình mặt cầu (S) có tâm O(0;0;0) bán kính R = 5
X, y, z tồn tại khi và chỉ khi d cắt (S)

Do đó P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Các biểu thức liên hệ giữa x, y, z có dạng phương trình mặt phẳng, mặt cầu. Từ đó giúp ta nghĩ đến việc xét vị trí tương dối giữa mặt cầu, với đường thẳng và mặt phẳng |

Ta có: \(\dfrac{x-1}{2}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
nên \(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
mà 2x+y-z=0
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}=\dfrac{2x+y-z-2+1+3}{4+3-5}=\dfrac{2}{2}=1\)
Do đó: x=3; y=2; z=8

ĐKXĐ: \(\left\{{}\begin{matrix}2020-y^2\ge0\\2020-z^2\ge0\\2020-x^2\ge0\end{matrix}\right.\)
Ta có:
\(x\sqrt{2020-y^2}+y\sqrt{2020-z^2}+z\sqrt{2020-x^2}=3030\)
\(\Leftrightarrow2x\sqrt{2020-y^2}+2y\sqrt{2020-z^2}+2z\sqrt{2020-x^2}=6060\)
\(\Leftrightarrow2020-y^2-2x\sqrt{2020-y^2}+x^2+2020-z^2-2y\sqrt{2020-z^2}+y^2+2020-x^2-2z\sqrt{2020-x^2}+z^2=0\)
\(\Leftrightarrow\left(\sqrt{2020-y^2}-x\right)^2+\left(\sqrt{2020-z^2}-y\right)^2+\left(\sqrt{2020-x^2}-z\right)^2=0\)
\(\Leftrightarrow\left(\sqrt{2020-y^2}-x\right)^2=\left(\sqrt{2020-z^2}-y\right)^2=\left(\sqrt{2020-x^2}-z\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2020-y^2}=x\\\sqrt{2020-z^2}=y\\\sqrt{2020-x^2}=z\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2020-y^2=x^2\\2020-z^2=y^2\\2020-x^2=z^2\end{matrix}\right.\)(vì \(x,y,z>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}2020=x^2+y^2\\2020=y^2+z^2\\2020=z^2+x^2\end{matrix}\right.\)
\(\Rightarrow2\left(x^2+y^2+z^2\right)=3.2020\)
\(\Rightarrow x^2+y^2+z^2=3.1010=3030\)
\(\Rightarrow A=x^2+y^2+z^2=3030\)
Vậy \(A=3030\)

Lời giải:
Áp dụng BĐT AM-GM:
\(x\sqrt{2020-y^2}+y\sqrt{2020-z^2}+z\sqrt{2020-x^2}\leq \frac{x^2+(2020-y^2)}{2}+\frac{y^2+(2020-z^2)}{2}+\frac{z^2+(2020-x^2)}{2}=3030\)Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} x^2=2020-y^2\\ y^2=2020-z^2\\ z^2=2020-x^2\end{matrix}\right.\Rightarrow x=y=z=\sqrt{1010}\)
Khi đó:
$A=3(\sqrt{1010})^2=3030$
Chọn đáp án A