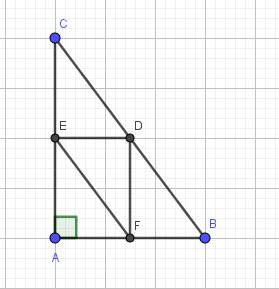
Cho tam giác ABC vuông tại A, có D là trung điểm của BC. Qua D vẽ DE ,DF lần lươt song song với AB,AC ( E thuộc AC, F thuộc AB)
a) Chứng minh tứ giác AEDF là hình chữ nhật.
b) Gọi M là điểm đối xứng với D qua AC. Chứng minh tứ giác AMCD là hình thoi.
c) Vẽ AH vuông góc với BC tại H. Chứng minh tứ giác HEFD là hình thang cân.
d) Gọi K là điểm đối xứng với A qua D. Tìm điều kiện của tam giác ABC để tứ giác ABKC là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Xét ΔABC có CF/CA=CD/CB
nên DF//AB và DF=AB/2
=>Di//AB và DI=AB
=>ABDI là hình bình hành

Để chứng minh các phần a, b và c, ta sẽ sử dụng các tính chất của tam giác vuông và hình chữ nhật.
a. Ta có tam giác ABC vuông tại A, nên theo định lí trung tuyến, ta có DE là đường trung tuyến của tam giác ABC. Do đó, DE song song với cạnh AC. Tương tự, ta có DF song song với cạnh AB. Vậy DE//AC và DF//AB.
b. Ta cần chứng minh AEDF là hình chữ nhật. Đầu tiên, ta thấy DE//AC và DF//AB (theo phần a). Khi đó, ta có:
- AD = DC (vì D là trung điểm của BC)
- AE = EB (vì E là trung điểm của AB)
- AF = FC (vì F là trung điểm của AC)
Vậy ta có các cạnh đối diện của tứ giác AEDF bằng nhau, do đó AEDF là hình chữ nhật.
c. Gọi M là điểm đối xứng của D qua AB. Ta cần chứng minh M đối xứng với N qua A. Để làm điều này, ta sẽ chứng minh AM = AN và góc MAN = góc NAM.
- Vì M là điểm đối xứng của D qua AB, nên ta có AM = AD.
- Vì N là điểm đối xứng của D qua AC, nên ta có AN = AD.
Do đó, ta có AM = AN.
- Ta có góc MAD = góc DAB (vì M là điểm đối xứng của D qua AB)
- Ta có góc NAD = góc DAC (vì N là điểm đối xứng của D qua AC)
Vì tam giác ABC vuông tại A, nên góc DAB = góc DAC. Từ đó, ta có góc MAD = góc NAD.
Vậy ta có AM = AN và góc MAN = góc NAM, do đó M đối xứng với N qua A.
Vậy ta đã chứng minh được M đối xứng với N qua A.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
giúp mình câu này nhé,ghi rõ ra cho mình luôn và cả hình nữa,cảm ơn mọi người

a/
DE//AB=> DE//AF
DF//AC=>DF//AE
=> AEDF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Hình bình hành AEDF có \(\widehat{A}=90^o\) => AEDF là hình chữ nhật
b/
DE//AB
DB=DC (1)
=> FA=FC (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại (2)
Từ (1) và (2) => DE là đường trung bình của ABC
\(\Rightarrow DE=\dfrac{BC}{2}=FB=FC\) (3)
DE//AB=> DE//FB (4)
Từ (3) và (4) => BFED là hình bình hành (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)
a) Do DE // AB (gt)
\(AC\perp AB\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DE\perp AC\)
\(\Rightarrow\widehat{DEA}=90^0\)
Do DF // AC (gt)
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DF\perp AC\)
\(\Rightarrow\widehat{DFA}=90^0\)
Tứ giác AEDF có:
\(\widehat{EAF}=\widehat{DEA}=\widehat{DFA}=90^0\)
\(\Rightarrow AEDF\) là hình chữ nhật
b) Do D là trung điểm BC (gt)
DF // AB (gt)
\(\Rightarrow F\) là trung điểm của AB
\(\Rightarrow FA=FB\)
Do AEDF là hình bình hành
\(\Rightarrow DE=AF\)
\(\Rightarrow DE=FB\)
Lại có:
DE // AB
\(\Rightarrow\) DE // FB
Tứ giác BFED có:
DE // FB (cmt)
DE = FB (cmt)
\(\Rightarrow BFED\) là hình bình hành
giải cho em với với ạ , giải rõ ra ạ :))