Cho số phức z thỏa mãn z = 1 m 2 + 2 m , trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = 2 i + 1 i + z ¯ − 5 + 3 i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
A. 3 2
B. 2 3
C. 3 5
D. 5 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
• Trước hết ta chứng minh được, với hai số ![]()
• Theo giả thiết
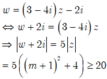

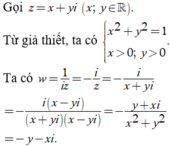
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-y;-x) (đều có hoành độ và tung độ âm). Đồng thời ![]()
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn C.

Chọn đáp án A
Giả sử số phức z = x + y i , x , y ∈ R có điểm biểu diễn là M(x;y)
Ta có 1 + z 2 = x + 1 2 - y 2 + 2 y x + 1 i là số thực nên
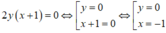
Vậy tập hợp các điểm M(x,y) biểu diễn số phức z = x +yi là hai đường thẳng y = 0; x = -1.
Đáp án C
Ta có:
w = 2 i + 1 i + z ¯ − 5 + 3 i = 2 i 2 + i + 2 i + 1 z ¯ − 5 + 3 i = − 7 + 4 i + 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 5 z ¯ = 5 z = 5 1 m 2 + 2 m
theo bất đẳng thức AM-GM, ta có:
1 m 2 + 2 m = 1 m 2 + m + m ≥ 3 1 m 2 . m . m 3 = 3 ⇒ r min = 3 5