Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
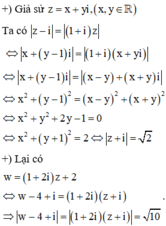
Suy ra, tập hợp điểm biểu diễn các số phức w là đường tròn


Đáp án C
Đặt z = x + yi , x ; y ∈ ℝ .
Đặt w = x ' + y ' i , x ' , y ' ∈ ℝ . Số phức w được biểu diễn bởi điểm M x ' ; y ' .
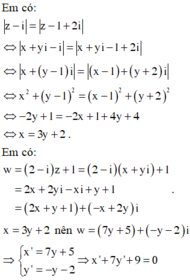
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7 y + 9 = 0. .

Giả sử z = x + yi có điểm M (x;y) biểu diễn z trên mặt phẳng (Oxy).
Ta có z - 1 + i = x - 1 + y + 1 i ; z + 1 - 2 i = x + 1 + - y - 2 i
Theo đề bài
z - 1 + i = z + 1 - 2 i ⇔ x - 1 2 + y + 1 2 = x - 1 2 + - y - 2 2 ⇔ x - 1 2 + y + 1 2 = x - 1 2 + y + 2 2 ⇔ x 2 - 2 x + 1 + y 2 + 1 = x 2 + 2 x + 1 + y 2 + 4 y + 4
Do đó tập hợp các điểm biểu diễn của z là đường thẳng ∆ : 4 x + 2 y + 3 = 0
Suy ra a = 4; b = 2; c = 3 Vậy ab + c = 11
Đáp án C

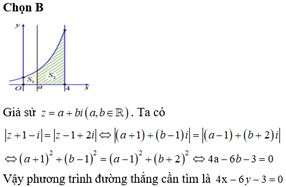
Đáp án B.
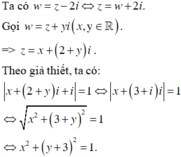
Vậy tập hợp các số phức w = z - 2i là đường tròn tâm I(0;-3).
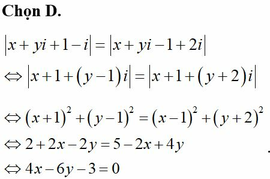
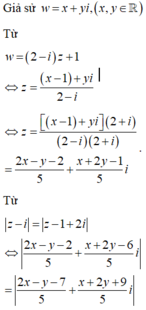
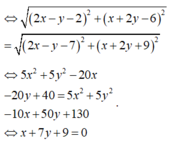


Chọn đáp án A
Giả sử số phức z = x + y i , x , y ∈ R có điểm biểu diễn là M(x;y)
Ta có 1 + z 2 = x + 1 2 - y 2 + 2 y x + 1 i là số thực nên
Vậy tập hợp các điểm M(x,y) biểu diễn số phức z = x +yi là hai đường thẳng y = 0; x = -1.